Математические задачи энергетики: Методические указания к выполнению контрольной работы, страница 4

Таблица 4

Выбор количества электроприемников n_j, их величины S_j и вероятности включения каждого Р_вj определяется по таблице 3 в соответствии с последней цифрой зачетной книжки.

Расчетная вероятностьР(Н) выбирается по первой букве фамилии из таблицы 4, при соответствующем номере варианта исходных данных.

Например. Иванов Николая Иванович. Зачетная книжка № 87354. Исходные данные для расчета:

n₁=3,   S₁=5,   P_в1=0,4;              n₂=2,   S₂=10,   P_в2=0,5;

n₃=4,   S₃=5,   P_в3=0,3;              n₄=3,   S₄=15,   P_в4=0,7;

Р(Н) > 15.

Методические указания по решению задачи № 2

Пусть K = 3,          n₁=3             S₁=10 кВ×А           р₁=0,7

n₂=2             S₂=15 кВ×А           р₂=0,6

n₃=4             S₃=5 кВ×А             р₃=0,5

Определить Р(Н > 15 кВ×А) - ?

Решение

Число случаев с нагрузкой более 15 кВ×А очень велико, поэтому выявляем все случаи, когда нагрузка головного участка .

.

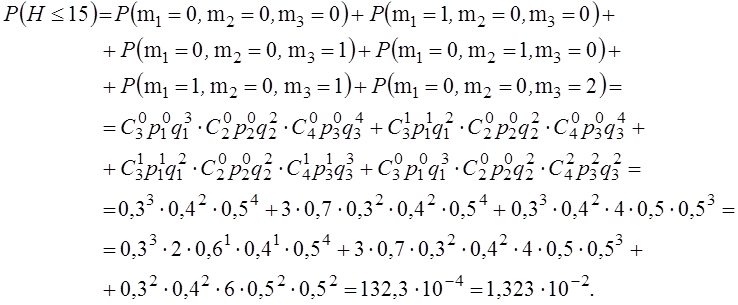
СТАТИСТИЧЕСКИЕ КРИТЕРИИ И ИХ ПРИМЕНЕНИЕ

Распределение Стьюдента (t - критерий)

Распределение Стьюдента даетвозможность находить генеральное среднее или проверять статистические гипотезы при очень малых выборках. Распределение Стьюдента определяется по формуле:

,

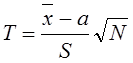где  - случайная величина, определенная на выборке объемом N;

а - математическое ожидание случайной величины;

S - среднее квадратическое отклонение, определенноена основе выборочной дисперсии S²;

N – объем выборки.

Очевидно, что распределение Т должно существенно зависеть от объема выборки или числа степеней свободы f=N-1, с которым определена S². При большихN  S² приближается к s ². Распределение Т симметрично относительноначала координат, т.е. . Квантили распределения Стьюдента для q = 0,05 приведены в таблице 5; при q ¹ 0,05  следует пользоваться более полными таблицами.

Таблица 5

Квантили распределения Стьюдента приq = 0,05