Математические задачи энергетики: Методические указания к выполнению контрольной работы, страница 9

Вид экстремума выбирается по последней цифре зачетной книжки: если цифра четная, то берется максимум, если нечетная - минимум.Значения коэффициентов функции цели выбираются по первой букве фамилии студента из таблицы 15. Коэффициенты в ограничениях выбираются по первой буквеимени из таблицы 16.

Таблица15

Таблица16

Продолжение табл. 16

Например, студент Сергеев Иван Петрович с зачетной книжкой № 86127 будет иметь следующее задание:

f = 25 - x₁ +5x₂   ® min

при

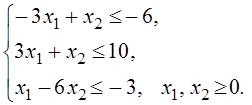
Методические указания по решение задачи № 4

Рекомендуется решить задачу сначала графически, так как в этом случае менее вероятны арифметические ошибки.

Решение задачи симплекс-методом полезно сверять на каждом шаге с графическим решением: каждая симплекс таблица должна соответствовать пересечению каких-либо ограничений. При это не следует забывать, чтооси координат, вследствие требования неотрицательности переменных также являются ограничениями.

Пример: Найти  x₁ иx₂ , которые максимизируют целевую функцию

F(x_i) = 2x₁ +3x₂   ® max

при условиях ограничений:

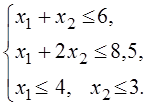
Задачу решить 1) графически; 2) симплекс-преобразованием; 3) с помощью симплекс-таблицы.

Решение

1)  графический метод

Целевая функция f = 0 + 2x₁ +3x₂   ® max

при условиях ограничений

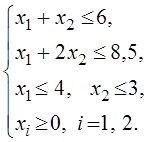
Строим в осях координат (прямоугольные)  x₁ и x₂   прямые, соответствующие условиям ограничений

x₁ +x₂  = 6                                                                (1)

x₁ +2x₂  = 8,5                                                           (2)

x₁ = 4                                                                        (3)

x₂  = 3                                                                       (4)

Каждое уравнение строим по двум координатам, определяемым исходя из пересечения осей.

Строим также F(x_i) = 2x₁ + 3x₂  = 6.