Математические задачи энергетики: Методические указания к выполнению контрольной работы, страница 14

Примечание: х – одна линия Лi;

                        хх – две цепи Лi;

- – цепь Лiотсутствует.

Таблица 23

Варианты источников питания

№ варианта	ИП1	ИП2	ИП3
1	х	-	-
2	-	х	-
3	-	-	х
4	х	-	х
5	-	х	х
6	х	х	-

Примечание: х – наличие источника питания;

-  – отсутствие источника питания.

Количество трансформаторов в узле подключения потребителя определяется по последней цифре зачетной книжке: четная – один трансформатор, нечетная – два трансформатора.

Пример для варианта 38 с двумя трансформаторами в узле 6

 

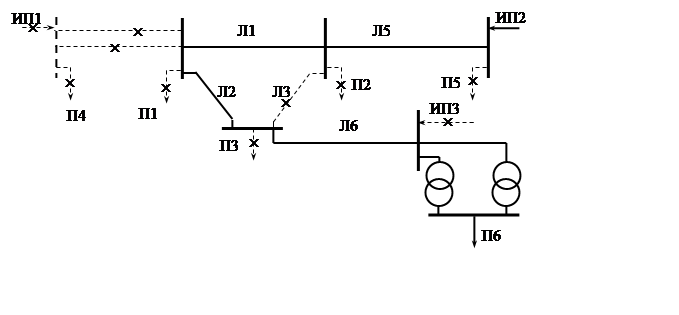Полученная конфигурация системы электроснабжения представляет технологическую схему, относительно узла 6 с одним источником питания.

Уравнения безотказной работы потребителя составляются на основании логических схем, полученных на основе логических рассуждений, ведущих к цели расчета надежности. Логические рассуждения в расчетах надежности бывают двух типов: - «по безотказности» и «по отказу».

Элементы системы электроснабжения в логических схемах расчета надежности будем обозначать символами R_i при логических рассуждениях «по безотказности» и символами F_i – «по отказу».

Для расчета безотказной работы потребителя, исходную схему (технологическую) заменим логической по условию «безотказной» работы, рис. 5, а по условию "отказа" – рис. 6.

 

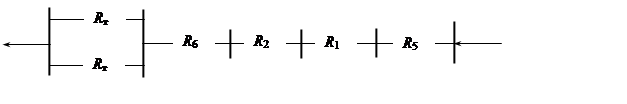Рис. 5. Логическая схема электроснабжения по условию

безотказной работы

Уравнение безотказной работы потребителя по условию "безотказности" в соответствии с логической схемой рис. 5 примет вид

R_S = R₅ × R₁ × R₂ × R₆ ×(R_т + R_т - R_т × R_т).

Если предположить, что трансформаторы однотипные, то R_S преобразуется:

R_S = R₅× R₁ × R₂ × R₆ ×(2R_т -).

 

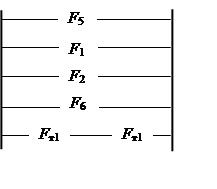Рис. 6. Логическая схема электроснабжения по условию отказа

Уравнение по условию отказа в соответствии с логической схемой рис. 6 примет вид:

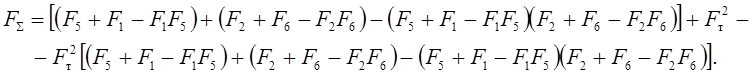
После алгебраических преобразований получим:

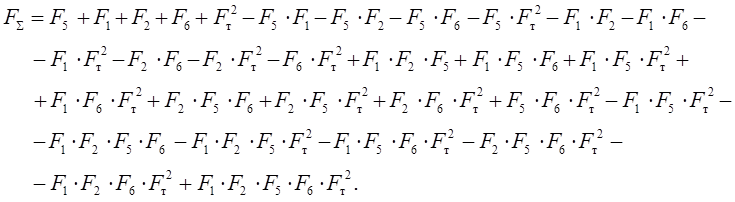
Поскольку состояния "безотказность" и "отказ" противоположны друг другу, то R_S + F_S = 1.

Проверим правильность составленных уравнений.

Выразим R_i = 1-F_i и поставим в R_S:

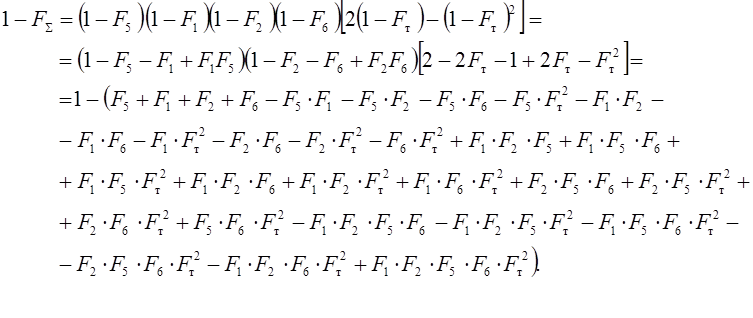
ЛИТЕРАТУРА

1. Электрические системы. Математические задачи энергетике. Под ред. В.А. Веникова. –М.: Высшая школа, 1981.

2. Коваленко И.Н. Теория вероятности и математическая статистика. –М.: Высшая школа, 1982.

3. Теория вероятности. Учебник для инженеров технических специальностей. Захаров В.К. и др. –М.: Наука, 1983.

4. Севастьянов Б.А. Курс теории вероятности и математической статистики. –М.: Наука, 1982.

5. Вентцель Е.С. Овчаров Л.А. Прикладные задачи теории вероятностей. –М.: Радио и связь, 1983.

6. Электроэнергетические системы в примерах к иллюстрациях. Под ред. В.А. Веникова. –М.: Энергоатомиздат, 1983.

.7. Вентцель Е.С. Исследование операций. –М.: Советское радио, 1973.

СОДЕРЖАНИЕ

Введение  ………………………………………………………………..
Теоремы теории вероятности  …………………………………………
Задача 1  …………………………………………………………………
Задача 2  …………………………………………………………………
Статистические критерии и их применение  …………………………
Задача 3  …………………………………………………………………
Задача 4  …………………………………………………………………
Задача 5  …………………………………………………………………