Математические задачи энергетики: Методические указания к выполнению контрольной работы, страница 2

Теорема умножения вероятностей

Вероятность произведения двух событий равна вероятности одного из них, умноженной на условную вероятность другого при наличии первого:

Р(АВ) = Р(А) × Р(В/А)

или

Р(АВ) = Р(В) × Р(А/В).

Для независимых событий А и В

Р(АВ) = Р(А) × Р(В).

Теорема умножения вероятностей для нескольких событий

Р(А₁А₂А₃…А_n) = Р(А₁)Р(А₂/А₁)Р(А₃/А₁А₂)…Р(А_n/А₁А₂…А_n-1).

В случае, когда события независимы, т.е. появление любого числа из них не меняет вероятностей появления остальных,

.

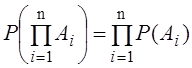Схема независимых испытаний

Опыты называются независимыми, если вероятность того или иного исхода каждого опыта не завесят от того, какие исходы имели другие опыты.

Независимые опыты могут производиться как в одинаковых условиях, так и в различных. В первом случае вероятность появления какого-либо события А во всех опытах одна и та же, во втором случае она меняется от опыта к опыту.

Если в одинаковых условиях производится n независимых опытов и в каждом из них с вероятностью р появляется событие А, то вероятность Р_m,n   того, что событие А произойдет в этих опытах ровно m раз выражается формулой

,

гдеq = 1-p.

Эта формула отражает биномиальное распределение вероятностей. Если условия опытов различны и вероятность события А в i-том опыте равнар_i (i =1, 2, ..., n), то вероятность Р_m,nтого, что событие А появится в этих опытах ровно m раз, равна коэффициенту при z^m - в разложении по степеням z производящей функции:

,

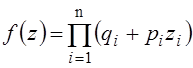гдеq_i = 1-p_i; z - произвольный параметр.

ЗАДАЧА № 1

Записать алгебраическое выражение вероятности соответствующего состояния электрической цепи АВ.

Состояния:   а) отказ цепи АВ,

б) безотказная работа цепи АВ.

Схема состояния электрической цепи АВ приведены на рис.1 .

Рекомендации по выбору варианта

Схема выбирается по первой букве фамилии из таблицы 1.

Состояние цепи - по последней цифре зачетной книжки: если четное - вариант а); если нечетное - вариантб).

Таблица 1

Буква	А, П	Б, Р	В, С	Г, Т	Д, У	Е, Ф	Ж, Х	З, Ц	И, Ч	К, Ш
№ сх.	1	2	3	4	5	6	7	8	9	10

Продолжение табл. 1

Буква	Л, Щ	М, Э	Н, Ю	О, Я	-
№ сх.	11	12	13	14	-

 

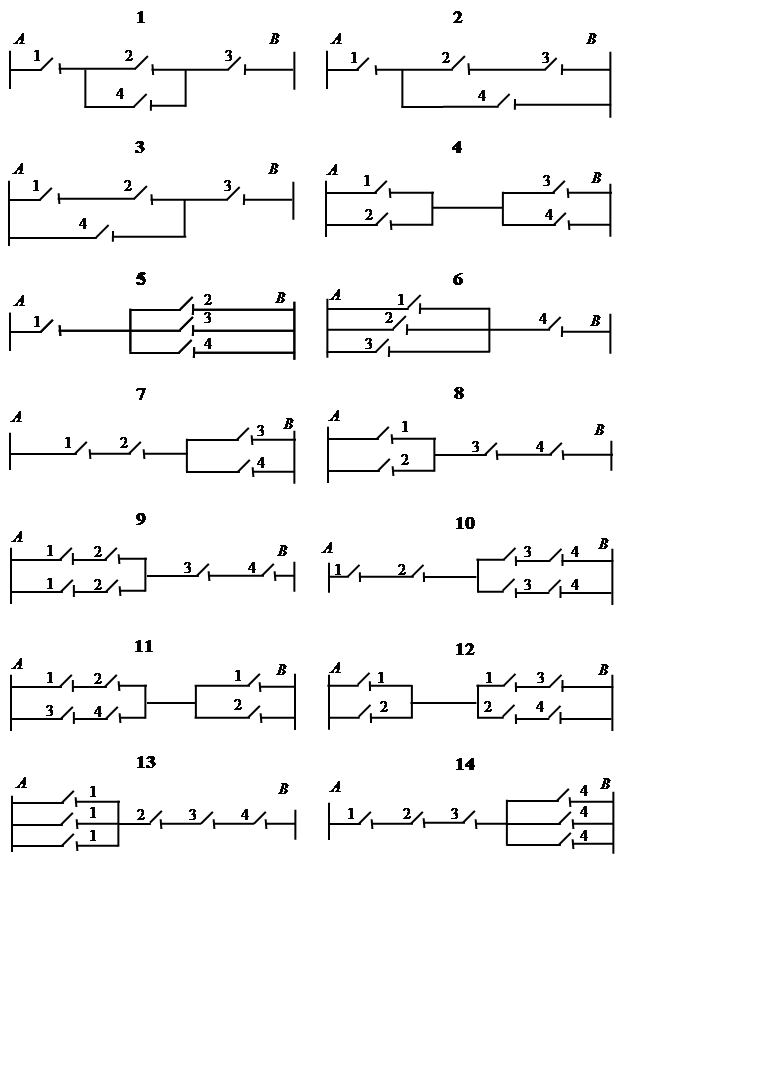
Рис. 1

Вероятность включения i-го контакта выбирается по таблице 2 в соответствии с последней цифрой зачетной книжки.

Например, студент Иванов В.В. имеет зачетную книжку № 870208. Следовательно, задание будет: Схема № 9, состояние а) - отказ цепи, вариант № 8: 1-р₁; 2-р; 3-р; 4-р₄.

Таблица 2

№ варианта	Вероятность включения контакта
	1	2	3	4
1	р1	р2	р3	р4
2	р1	р1	р2	р2
3	р	р	р	р
4	р3	р3	р4	р4
5	р2	р2	р3	р3
6	р	р	р3	р4
7	р1	р2	р	р
8	р1	р	р	р4
9	р	р2	р3	р
0	р1	р2	р4	р4

Методические указания к решению задачи № 1

Записать алгебраическое выражение вероятности безотказного состояния для приведенной схемы

 

Решение

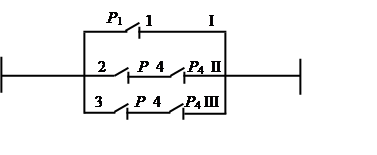Безотказное состояние цепи может быть представлено некоторым количеством независимых несовместных событий, в которых будет обеспечиваться одновременно совместное включенное и отключенное состояние различных контактов, например, включенный контакт 1 и отключенные контакты 2, 3 и 4.