Математика \ Математические задачи энергетики

Математические задачи энергетики: Методические указания к выполнению контрольной работы, страница 3

Для записи соответствующих противоположных состояний примем обозначсения для контактов: включен контакт, например, 1 и отключен контакт - . Контакт 4 имеется во второом и третьем участках, поэтому обозначим их 4 и 4¢ соответственно включены, и и  - отключены.

Вероятность i-го ранее указанного состояния будет иметь вид

.

На основании теоремы умножения независимых событий Рiбудет определяться выражением

.

В последнее выражение можно подставить исходные данные вероятности соответствующих контактов

Рi = р1(1-р)(1-р4)(1-р)(1-р4) = р1(1-р)2(1-р4)2.

Представим все возможные состояния, обеспечивающие безотказность цепи:

1:     ;

2:     ;

3:      ;

4:      ;

5:      ;

6:      ;

7:      ;

8:      ;

9:      ;

10:    ;

11:    ;

12:    ;

13:    ;

14:    ;

15:    ;

16:    ;

17:    ;

18:    ;

19:    ;

20:    ;

21:    .

Вероятность безотказности цепи будет равна сумме вероятности перечисленных состояний.

.

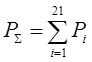После преобразований приведенных выражений получим

.

ЗАДАЧА № 2

От магистральной кабельной линии в цеху промышленного предприятия получают питание k групп электродвигателей (n1, n2, ..., nk)с потребляемой мощностью: 1) a×S1 кВ×А, n1=а; 2) b×S2 кВ×А, n1=b; 3) …; nn=k; … и одинаковым cosj. Вероятность включения в работу каждого двигателя в группах соответственно рi (p1, p2, ..., pk). События включения в работу и отключения каждого двигателя в каждой группе – независимые.

Требуется определить вероятности нагрузки головного участка линии;

а) Н1 = 0;

б) ;

в) .

Решение

Для определения вероятностей нагрузки головного участка используем схему независимых испытаний - биномиальный закон распределения.

а) Вероятность, нагрузки головного участка, равная нулю, определяется при условии, что не включен ни один двигатель (в этом случае mi=0).

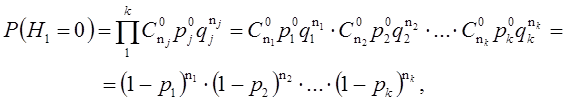
где     (1-рi) - вероятность отключенного состояния i-го двигателя;

 - число сочетаний из  n  элементов по m.

Для выполнения пунктов б) и в) необходимо выявить все случаи, когда нагрузка головного участка равна и больше (меньше) S1 и определить эти вероятности.

Вероятность нагрузки головного участка Р() или Р() определяется по выражениям:

,

,

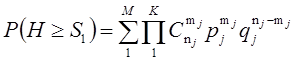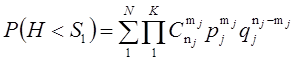где     М – количество случаев удовлетворяющих условию Н ³ S1;

          N – количество случаев удовлетворяющих условию Н < S1.

Если число случаев очень велико, то задачу рекомендуетсярешить, учитывая противоположное состояние.

Рекомендации по выбору варианта

 


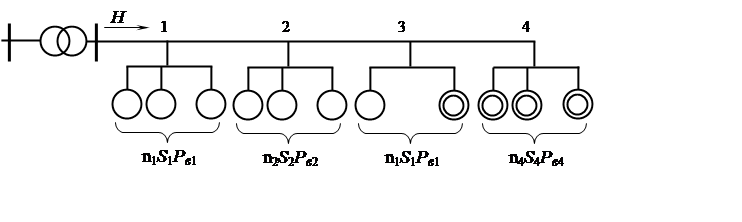Рис. 2

Таблица 3

№

вар.

1

2

3

4

n1

S1

Pв1

n2

S2

Pв2

n3

S3

Pв3

n4

S4

Pв4

1

2

3

0,5

3

4

0,6

4

5

0,7

2

7

0,4

2

4

3

0,4

5

5

0,3

3

2

0,6

2

5

0,6

3

2

10

0,3

3

5

0,4

3

15

0,5

4

10

0,6

4

3

5

0,4

2

10

0,5

4

5

0,3

3

15

0,7

5

2

3

0,8

3

5

0,4

4

2

0,6

5

5

0,4

6

5

10

0,7

3

5

0,6

2

15

0,5

4

5

0,4

7

4

15

0,6

6

10

0,5

3

15

0,4

2

10

0,7

8

2

7

0,5

4

5

0,4

6

3

0,7

3

4

0,6

9

3

15

0,4

2

10

0,7

4

15

0,6

6

10

0,5

0

5

5

0,6

3

5

0,6

2

3

0,2

4

2

0,4
Скачать файл