Математические задачи энергетики: Методические указания к выполнению контрольной работы, страница 10

Решение: F(x_i) = 14,5-max при x₁ = 3,5,  x₂  = 2,5.

 

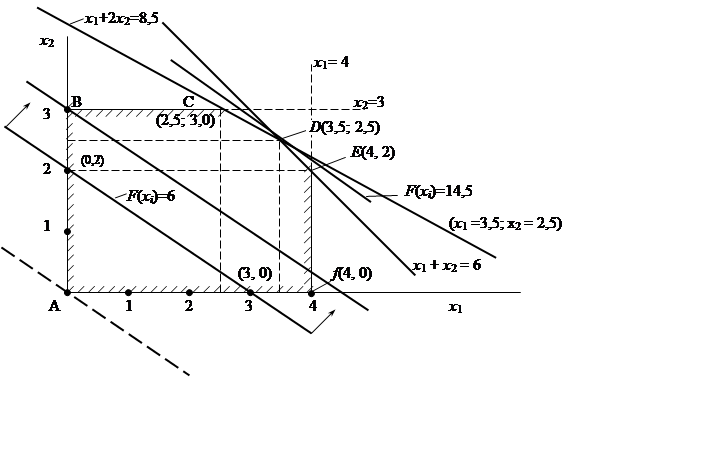Рис. 3

2) симплекс-преобразование

Запишем целевую функцию и условия ограничений в каноническом виде:

-F = -2x₁  - 3x₂      ® min

-F = 0-(2x₁  + 3x₂) ® min

         ® 

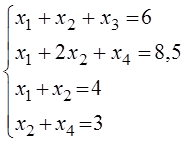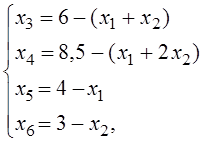
где x₃ ¸ x₆  - дополнительно введенные неизвестные - обозначим их базисными; а x₁  и x₂   - свободные переменные.

Найдем значения базисных переменных и значение функции цели при равенстве нулю свободных переменных: x₁ = 0;  x₂ = 0.

F(x_i) = 0,  x₃ = 6,  x₄ = 8,5,  x₅ = 4,  x₆ = 3 - это одно из базисных решений и соответствует одной из вершин выпуклого многоугольника (точка А).

Задача заключается в том, чтобы переходя от одной вершины к другой, функция цели ® min.

Поскольку можно изменять свободные переменныеx₁  или x₂ , то наибольшее воздействие окажет, если мы изменим x₂ , т.к. у него коэффициент больше чем при  x₁ .  x₂  будет увеличивать до тех пор, пока одна из базисных переменных не обратится в нуль.

x3 = 0     при     x2 = 6 x4 = 0                x2 = 4,25 x5        не зависит от x2  x6 = 0    если    x2 = 3

Меняем переменные там, где x2  самое минимальное x2  ® базисная; x6  ® свободная x2  = 3 - x6

          x₁  и x₆ - свободные переменные.

Выразим базисные переменные и F(x_i)  через новые свободные переменные:

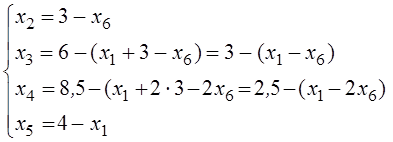
-F = 0 - (2x₁ + 3×3 - 3x₆) = - 9 - (2x₁ - 3x₆).

Находим значения базисных переменных и функции цели при равенстве нулю свободных переменных

-F₂ = -9 < F₁ = 0

x₁ = 0,  x₂ = 3,  x₃ = 3,  x₄ = 2,5,  x₅ = 4,  x₆ = 0                     (точка В).

Это решение можно еще улучшить, т.к. в функции цели есть положительный коэффициент приx₁ , поэтому будем увеличивать x₁  до тех пор, пока одна из базисных переменных не обратится в нуль.

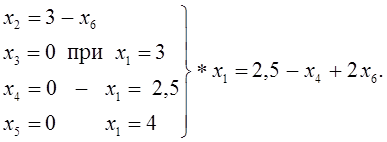
В качестве свободных переменных принимаем  x₄  и  x₆ ,  через которые и выразим условия ограничений и F(x_i).

х₁ = 2,5 - х₄ + 2х₆

х₂ = 3 - х₆

х₃ = 3 - 2,5 + х₄ - 2х₆ + х₆ = 0,5 + х₄ - х₆ 

х₅ = 4 - 2,5 + х₄ - 2х₆ = 1,5 + х₄ - 2х₆ 

-F(x) = -9 - (5 - 2х₄ + 4х₆ - 3х₆) = -14 -(-2х₄ + х₆).

Новое решение имеет вид:

-F(x) = -14

при

х₁ = 2,5, х₂ = 3, х₃ = 0,5,

х₄ = 0, х₅ = 15, х₆ = 0                 (точка С).

Но в функции цели при х₆  есть положительный коэффициент:

х₁       ®      0        при    х₆ = -1,25

х₂       ®      0        при    х₆ = 3

х₃       ®      0        при    х₆ = 0,5*

х₅       ®      0        при    х₆ = 0,75

Делаем замену х₆  ®  х₃:

х₆ = 0,5 + х₄ – х₃;

х₁ = 2,5 – х₄ + 2×0,5 + 2х₄ – 2х₃ = 3,5 + х₄ – 2х₃;

х₂ = 3 – 0,5 – х₄ + х₃ = 2,5 – х₄ + х₃;

х₅ = 1,5 + х₄ – 2(0,5 + х₄ – х₃) = 0,5 – х₄ + 2х₃;

–F(х_i) = 14 – (– 2х₄ + 0,5 + х₄ – х₃) = –14,5 – (– х₄ – х₃).