Вычислительная математика: Методические указания к практическим и лабораторным работам, страница 6

Таблица 3.3

МЕТОД ЗЕЙДЕЛЯ
K	XT(1)	X(1) н. у. Х=0	X(1) н.у. X=BET
0	2,000000	0,000000	4,759183
1	2,000000	4,759183	2,094929
2	2,000000	2,173193	2,002068
3	2,000000	2,008807	2,000145
4	2,000000	2,000477	2,000145
5	2,000000	2,000026	2,000145

Методические указания

1. Основные теоретические положения, необходимые для выполнения работы

          Методы решения САУ подразделяются на прямые (точные) и итерационные (приближенные). Прямые методы позволяют получить точное решение за конечное число арифметических операций. Наибольшее применение среди прямых методов получил метод Гаусса.

          Итерационные методы за конечное число итераций позволяют получать искомое решение с некоторой погрешностью e. Ниже приведены алгоритмы Зейделя и наискорейшего спуска, используемые в работе для решения САУ вида

,

      

          Метод Зейделя

         

 

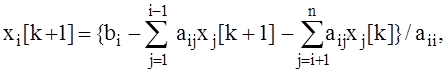
где  - i-я компонента вектора x на k-й итерации, , i[1, n] - начальные условия, которые рекомендуется задавать в виде , i[1, n].

          Метод Зейделя будет сходиться к единственному решению при выполнении условия

 ,   .

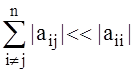          Метод наискорейшего спуска

,   ,

,   k = 0, 1, ... ,

,      ,

                 

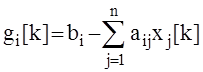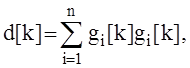
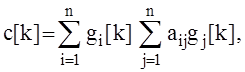
где - i-я компонента вектора  x  на  k-й  итерации, , i[1, n] - начальные условия, которые задаются, например, в виде = 0, i[1, n].

          Метод наискорейшего спуска сходится к единственному решению, если матрица A - симметрическая, положительно определенная.

          В общем случае для неособенной матрицы A можно предусмотреть условие сходимости метода путем первой трансформации Гаусса исходной САУ

,

где матрица - симметрическая, положительно определенная.

2. Подпрограммы, необходимые для выполнения работы

Подпрограммы

SUBROUTINE N1YMGS (A,B,N,G,X),

SUBROUTINE N1YMNS (A,B,N,G,X)

реализуют алгоритмы решения САУ методами Зейделя и наискорейшего спуска (одна итерация) соответственно.

          Входные параметры подпрограмм:

          А(N,N) -  (N ´ N)-мерная матрица САУ;

          B(N) -  N-мерный вектор правой части САУ;

          N        -  мерность САУ;        

G(N) -  N-мерный вектор невязки (g = b - Ax);

          X(N) -  N-мерный вектор начальных условий решения САУ.

          Выходные параметры подпрограммы:

          X(N) -  N-мерный вектор уточненных значений решения САУ.

          Подпрограмма

SUBROUTINE N1YGAU (A,B,X,N)

реализует алгоритм метода Гаусса с выбором главного элемента.

          Входные A, B, N и выходной X параметры подпрограммы N1YGAU совпадают по описанию с аналогичными параметрами в подпрограммах N1YMGS, N1YMNS.

          В подпрограмме N1YGAU матрица A приводится к треугольной, т.е. исходная матрица A портится, поэтому при составлении головной программы необходимо иметь этот факт в виду.

          Подпрограмма

SUBROUTINE N1YTGA (A,B,N,AT,U,V)

реализует процедуру первой трансформации Гаусса.

          Входные параметры подпрограммы:

          А(N,N) - (N ´ N)-мерная матрица САУ;

          B(N) - N-мерный вектор правой части САУ;

          N      - мерность САУ;

          Промежуточные параметры подпрограммы:

          АТ(N,N) - (N ´ N)-мерная матрица транспонированная относительно исходной матрицы САУ.

          Выходные параметры подпрограммы:

          U(N,N) - (N ´ N)- мерная матрица, определяемая произведением транспонированной матрицы САУ на исходную;

          V(N) - N-мерный вектор правой части, определяемый произведением транспонированной матрицы САУ на исходный вектор правой части САУ.

Контрольные вопросы

          1. Принципы построения итерационных методов.

          2. Метод последовательных приближений.

          3. Метод Зейделя.

          4. Метод наискорейшего спуска.