Математика \ Вычислительная математика

Вычислительная математика: Методические указания к практическим и лабораторным работам, страница 12

K

X1

X2

X3

 0

0,3000D+00

0,2000D+01

0,2500D–01

1

0,6743D+00

0,1411D+01

0,7813D+00

2

0,9430D+00

0,1053D+01

0,5343D+00

3

0,1073D+01

0,8257D+00

0,3519D+00

¼

9

0,1200D+01

0,5000D+00

0,1000D+00

          3. Решить нелинейную систему алгебраических уравнений методом Ньютона с параметрами DK = 2,0 и e = 10–5 и сохранить файл sx.dat, формируемый в подпрограмме, реализующей алгоритм решения системы уравнений, в который записывается процедура сходимости корней системы уравнений (см. табл. 5.2).

          4. Повторить пп 1, 2, 3, решая систему уравнений методом наискорейшего спуска. Сравнить результаты.

          5. Оформить отчет.

          Примечания:

          1) при выполнении работы студенты должны составить головную программу, в которой необходимо осуществить:

          a) ввод исходных данных (номер варианта, параметров DK и e),

          б) обращение к подпрограмме N1YIRU, в которой задаются порядок n и корни xi, i Î[1, n] системы уравнений,

          в) обращение к подпрограмме N1YNU, где по вводимому значению параметра DK выбираются начальные условия xi0, i Î[1, n] искомых корней системы (см. п. 1 "Порядок выполнения работы"),

          г) обращение к подпрограмме N1YNTM (N1YNSM), в которой реализован метод Ньютона (метод наискорейшего спуска) решения нелинейной алгебраической системы,

          д) обращение к подпрограмме N1YPGR для вычисления погрешностей найденного решения,

          е) запись полученных результатов в файлы данных (см. табл. 5.1 ¸ 5.2);

          2) все расчеты в подпрограммах производятся с удвоенной точностью, следовательно вещественные данные в головной программе должны быть описаны как REAL*8.

Содержание отчета

          1. Цель работы.

          2. Постановка задачи.

          3. Метод Ньютона, метод спуска.

          4. Листинг головной программы.

          5. Результаты вычислений (см. табл. 5.1 ¸ 5.2).

          6. Графики зависимостей:

          1) lg Eмо = f(DK) (lg Eсо = f(DK)), KM = f(DK),

          2) lg Eмо = f(lg e) (lg Eсо = f(lg EPS)), KM = f(lg EPS),

          3) = f(K), KÎ [0, KM], KM – количество итераций для вычисления корней с заданными DK и EPS.

          7. Выводы.

Методические указания

1. Основные теоретические положения, необходимые для выполнения работы

          Метод Ньютона. Если в некоторой области, содержащей решение
  системы

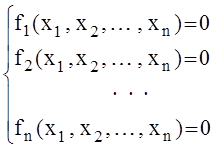
функции fi(x), i Î[1, n] непрерывны, имеют непрерывные частные производные и в точке x =  ( матрица

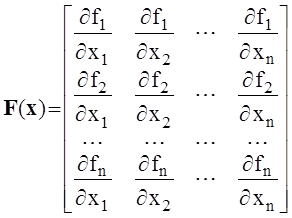
не вырождена, то решение может быть определено посредством итерационной

процедуры метода Ньютона

xk+1 = xk – F–1(xk)f(xk),   k = 0, 1, 2, ... ,

f(xk) = {f1(xk), f2(xk), ... , fn(xk)}.

          Условием сходимости метода Ньютона, помимо требований предъявляемых к функциям fi(x), iÎ [1, n] и матрице F(x), является соответствующий выбор начальных условий. Вектор x0 должен быть выбран достаточно близко к истинному решению x*.

          В лабораторной работе для решения нелинейной системы уравнений используется модификация приведенного метода Ньютона, в которой операция обращения матрицы заменяется процедурой решения системы n линейных алгебраических уравнений. Данный алгоритм реализуется в следующем виде

xk+1 = xk + Dxk,   k = 0, 1, 2, ... ,

а Dxk = xk+1 – xk представляет собой решение линейной системы

F(xk)Dxk = - f(xk),

полученной путем элементарных преобразований исходного алгоритма.

          Останов итерационной процедуры метода Ньютона можно осуществлять по соотношению

| | £ e,   k = 0, 1, 2, …,

где e > 0 – сколь угодно малое, наперед задаваемое число.

          Достоинством метода Ньютона является очень высокая скорость сходимости, а недостатком – большая чувствительность к начальным условиям, т.к. при их очень грубом задании алгоритм может разойтись или привести к другому решению.

Скачать файл