Вычислительная математика: Методические указания к практическим и лабораторным работам, страница 2

Методические указания

1. Основные теоретические положения, необходимые для выполнения работы

          Для заданной на  [a, b]  в узлах интерполяции   функции y = f(x) коэффициенты интерполяционного полинома  могут быть определены из системы линейных алгебраических уравнений, формируемых в узлах интерполяции в виде

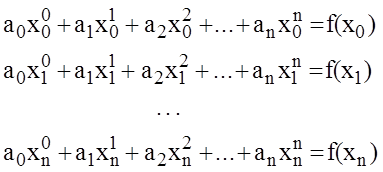
          Данная система имеет единственное решение, поскольку ее определитель есть определитель Вандермонда и он не равен нулю, а следовательно, искомое решение может быть найдено прямыми алгоритмами вычислительной математики, например методом Гаусса.

          Погрешности интерполирования предлагается определять по метрикам пространств  и , а именно, если

то в пространстве на [a, b]

eм =,        eмо = eм / | f() |,

где - значение x, при котором имеет место eм,

а в пространстве  на [a, b]

,          .

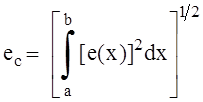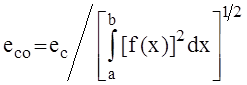2. Подпрограммы, необходимые для выполнения работы

Подпрограмма

SUBROUTINE N1YSAU (N,X,Y,U,V)

формирует систему линейных алгебраических уравнений (САУ).

          Входные параметры подпрограммы:

          N    - количество узлов интерполяции;

          X(N) - N-мерный массив значений узлов интерполяции;

          Y(N) - N-мерный массив значений функции в узлах.

          Выходные параметры подпрограммы:

          U(N,N) - (N ´ N)-мерная матрица сформированной САУ;

          V(N) - N-мерный вектор правой части САУ.

          Подпрограмма

SUBROUTINE N1YGAU (A,B,X,N)

осуществляет решение САУ.

          Входные параметры подпрограммы:

          A(N,N) - (N ´ N)-мерная матрица САУ;

          B(N) - N-мерный вектор правой части САУ;

          N      - мерность САУ.

          Выходные параметры подпрограммы:

          X(N) - N-мерный вектор решения САУ.

          Подпрограмма

SUBROUTINE N1YEEE (X,X1,N,E,EM,ES,EP,EMO,ESO,EPO)

осуществляет вычисление погрешностей.

          Входные параметры подпрограммы:

          X(N) - N-мерный массив истинных значений функции;

          X1(N) - N-мерный массив приближенных значений функции;

          N     - размерность массивов X и X1.

          Выходные параметры подпрограммы:

          E(N) - N-мерный массив погрешностей;  

EM   - максимальная погрешность;

          ES    - среднеквадратичная погрешность;

          EP    - среднее значение погрешности;

          EMO  - максимальная относительная погрешность;

          ESO   - среднеквадратичная относительная погрешность;

          EPO   - относительное среднее значение погрешности.

          Листинги используемых подпрограмм приведены в приложении.

Контрольные вопросы

          1. Методика синтеза интерполяционного полинома. Полином Лагранжа.

          2. Интерполяционные полиномы Ньютона.

          3. Остаточный член интерполяционной формулы Лагранжа.

          3. Рекомендации к использованию интерполяционных полиномов.

          4. Погрешности интерполяции, способы их оценивания.

          5. Влияние вида интерполируемой функции, количества и расположения узлов интерполирования на погрешности интерполяции.

2.ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ

Цель работы

          Ознакомиться с квадратурными формулами Ньютона-Котеса численного интегрирования, исследовать влияние порядка точности квадратурной формулы и шага интегрирования на точность вычисления определенного интеграла.

Постановка задачи

          Вычислить определенный интеграл

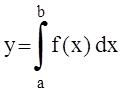,    a=0,  b=8

от функции  f(x), заданной на  [a, b]  с шагом   (= 0,1,  0,2,  0,4), посредством квадратурных формул:

          m = 0 - формула прямоугольников (левых прямоугольников);

          m = 1 - формула трапеций (Ньютона-Котеса первого порядка точности);

          m = 2 - формула парабол (Ньютона-Котеса второго порядка точности);

          m = 3 - формула "трех восьмых" (Ньютона-Котеса третьего порядка точности);

          m = 4 - формула Ньютона-Котеса четвертого порядка точности.

          Исследовать влияние шага дискретизации  функции f(x) на точность вычисления интеграла.