Вычислительная математика: Методические указания к практическим и лабораторным работам, страница 3

          При вычислении погрешностей интегрирования e = |yт – y| за точное значение интеграла yт следует принять его значение, вычисленное с минимальным шагом и максимальным порядком точности m квадратурной формулы.

Порядок выполнения работы

1. Ознакомиться с описанием работы. Уяснить цель и смысл задачи согласно

 варианту (табл. 2.1)

Таблица2.1

№	f(x)	№	f(x)
1		6
2		7
3		8
4		9
5		10

        2. Вычислить на [a, b] массив функции f(x) с заданным шагом .

3. Вычислить значение определенного интеграла от полученной реализации

f(x) по квадратурным формулам различного порядка точности m. Определить погрешности интегрирования.

4. Изменить шаг дискретизации  и повторить пп. 2 и 3.    

5. Оформить отчет.

Примечания:

1) пункт 3 выполняется по алгоритмам, реализованным в подпрограмме

N1YINK, листинг которой приведен в приложении;

2) при выполнении работы студенты должны составить головную программу,  в которой необходимо осуществить:

a) ввод данных,

б) вычисление на [a, b] с шагом массива функции f(x),

в) обращение к указанной в п.1 примечания подпрограмме,

        г) вычисление погрешностей интегрирования , где , i = 1, 2, …-

значения интегралов, вычисленных с шагом для порядка точности m квадратурной формулы,        

д) вывод полученных результатов в файлы с целью их визуализации, что

осуществляется с помощью специальной программы GRAF;

3) образцы заполнения файлов результатов приведены в виде табл. 2.2 2.4;

4) изменение параметров m и можно организовать в циклах – внешнем

по и вложенном по m.

Таблица 2.2                                                                                      Таблица 2.3

Таблица 2.4

DX	E (M=1)	E (M=2)	E (M=3)	E (M=4)	E (M=5)
0,10	0,1402E+00	0,3071E-03	0,1526E-04	0,3815E-04	0,0000E+00
0,20	0,2811E+00	0,1272E-02	0,2270E-03	0,1545E-02	0,1431E-03
0,40	0,5654E+00	0,5770E-02	0,1455E-02	0,1886E-02	0,9155E-03

Содержание отчета

1. Цель работы.

2. Постановка задачи.

3. Квадратурные формулы для m = 0; 1; 2.

4. Листинг программы.

5. Результаты вычислений (см. табл. 2.2 2.4).

6. Графики функции f(x) и погрешностей e = f(m) (для всех = const), e =

f() (для всех m = const).    

7. Выводы.

Методические указания

1. Основные теоретические положения, необходимые для выполнения работы

В основе численного интегрирования лежит приближенное вычисление площади под кривой, описываемой подынтегральной функцией.

В простейшем случае, если требуется вычислить

,

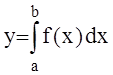площадь, ограниченную функцией f(x), можно представить в виде площади прямоугольника со сторонами (b - a) и f(a) (один из вариантов: f(a) - левых, f[(a + b)/2] - средних, f(b) - правых прямоугольников). Тогда

.

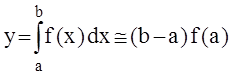Возникающая при этом погрешность может быть оценена как остаточный член интерполяционной формулы Лагранжа  (m = 0)