Вычислительная математика: Методические указания к практическим и лабораторным работам, страница 11

производит вычисление максимальной и максимальной относительной погрешностей между действительными и мнимыми частями истинных комплексных корней и их оценками.

          Входные параметры подпрограммы:

          PI(N) – N–мерный комплексный массив истинных корней;

          P(N)  – N–мерный комплексный массив оценок корней;

          N – количество комплексных корней.

          Выходные параметры подпрограммы:

          EM – максимальная погрешность между действительными и мнимыми частями истинных комплексных корней и их оценками;

          EMO – максимальная относительная погрешность между действительными и мнимыми частями истинных комплексных корней и их оценками.

          ESO – среднеквадратичная относительная погрешность между истинными корнями уравнения и их оценками.

          Листинги описанных подпрограмм приведены в приложении.

Контрольные вопросы

          1. Отделение корней алгебраического уравнения.

          2. Уточнение корней методом дихотомии.

          3. Уточнение корней методом Ньютона.

          4. Метод спуска.

          5. Решить алгебраическое уравнение 3–го порядка с вещественными корнями методом Ньютона.

5. РЕШЕНИЕ НЕЛИНЕЙНОЙ СИСТЕМЫ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ

Цель работы

          Исследование итерационных методов Ньютона и наискорейшего спуска решения нелинейной системы алгебраических уравнений. Анализ влияния начальных условий и параметра останова на точность (количество итераций) определения корней, сравнение методов решения.

Постановка задачи

          Решить нелинейную алгебраическую систему уравнений:

          1)

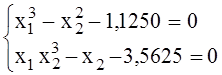
          Корни системы:   =  1,5; =  1,5.

          2)

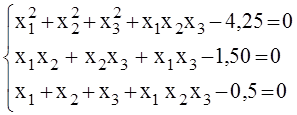
          Корни системы: =  2,0; = – 1,0; =  0,5.

          3)

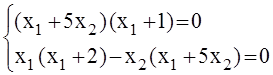
          Корни системы: = – 2,0; =  0,4.

          4)

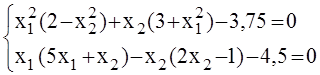
          Корни системы: = – 1,0; =  0,5.

          5)

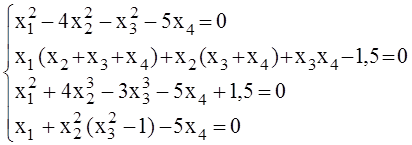
          Корни системы: =  2,0; = – 0,5; =  1,0; =  0,4.

6)

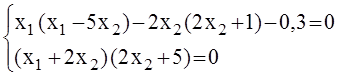
          Корни системы: = – 0,6; =  0,35.

          7)

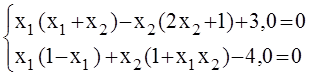
          Корни системы: =  3,0; = – 2,0.

          8)

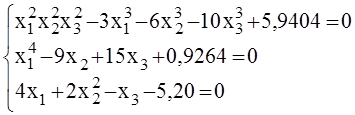
          Корни системы: =  1,2; =  0,5; =  0,1.

          9)

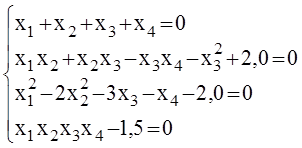
          Корни системы: = 2,0; = – 1,0; =  0,5; = – 1,5.

          10)

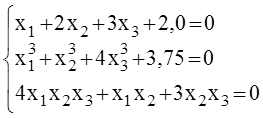
          Корни системы: = – 1,5; =  0,5; = – 0,5.

Порядок выполнения работы

1.  Решить нелинейную систему алгебраических уравнений методом Ньютона

с различными начальными условиями (изменять параметр DK, задающий начальные оценки корней в виде  или  ,  iÎ[1, n] от DK_min= 1,5 до DK_max= 4,0 с шагом HDK = 0,5),  положив параметр останова  e = const = 10^–3. Результаты зафиксировать в файл, образец которого показан в виде табл. 5.1.

2.  Решить нелинейную систему алгебраических уравнений методом Ньютона с фиксированным значением коэффициента DK = 2,0, изменяя значение параметра останова итерационной процедуры от величины  e₀ = 10^–9 до e_K = 10^–1 в виде  e_i+1 = e_i ×10, i Î[0, K–1]. Результаты зафиксировать в файл подобный тому, что приведен в табл. 5.1.

Таблица 5.1

Влияние начальных условий (параметра DK)

на точность и количество итераций метода Ньютона

DK	EPS	lgEPS	Eмo	lgEмo	Eсo	LgEсo	KM
1,50	0,1D–02	–3,0	0,2691D–06	–6,570	0,4687D–07	–7,329	7
2,00	0,1D–02	–3,0	0,5453D–04	–4,263	0,9497D–05	–5,022	7
2,50	0,1D–02	–3,0	0,6312D–06	–6,200	0,1099D–06	–6,959	8
3,00	0,1D–02	–3,0	0,2109D–04	–4,676	0,3672D–05	–5,435	8
3,50	0,1D–02	–3,0	0,7311D–07	–7,136	0,1273D–07	–7,895	9
4,00	0,1D–02	–3,0	0,2436D–05	–5,613	0,4244D–06	–6,372	9

Таблица 5.2

Сходимость метода Ньютона при DK = 2, EPS = 10^–5