Математика \ Вычислительная математика

Вычислительная математика: Методические указания к практическим и лабораторным работам, страница 5

№

15

A

0,380

  - 0,050

0,010

0,020

0,070

0,052

0,595

0,000

   - 0,040

0,040

0,030

0,000

0,478

   - 0,140

0,080

0,060

0,126

0,000

0,470

   - 0,020

0,250

0,000

0,090

0,010

      0,560

1

b

   - 2,140

1,833

1,736

   - 1,242

1,440

2

0,750

   - 0,858

3,160

   - 1,802

2,910

3

2,320

2,544

3,238

1,534

0,120

4

2,110

3,407

1,432

0,480

2,250

5

1,520

   - 1,269

3,500

   - 2,988

3,390

610

A

0,490

0,000

  - 0,128

0,090

0,150

   - 0,030

0,320

0,000

   - 0,061

0,020

0,010

   - 0,090

0,580

0,011

0,035

0,030

0,000

   - 0,073

0,580

0,000

0,020

   - 0,030

0,145

   - 0,012

0,420

6

b

0,964

1,279

   - 1,799

   - 4,971

2,153

7

1,564

   - 1,733

1,393

1,744

   - 2,046

8

2,332

   - 2,261

   - 1,484

0,932

1,758

9

1,946

0,805

1,935

2,741

2,905

10

2,810

0,236

2,859

0,047

1,157

,

где 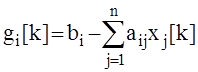,           i[1, n],   k = 1, 2, 3, …,

          в) вывод полученных результатов в файл с целью их визуализации, что выполняется с помощью специальной программы GRAF;

          4) образцы заполнения файлов результатов приведены в виде табл. 3.2, 3.3.

Содержание отчета

          1. Цель работы.

          2. Постановка задачи.

          3. Алгоритмы (в общем виде) методов Зейделя и наискорейшего спуска.

          4. Листинг программы.

          5. Результаты вычислений.

          6. Графики сходимости корня   итерационных методов в виде  (k - номер итерации) для   и .

          7. Выводы.

                                                                                                                        Таблица 3.2

МЕТОД ЗЕЙДЕЛЯ: с нач. условиями X(I)=0, I=1,N

K

X(1)

X(2)

X(3)

X(4)

X(5)

0

0,00000

  0,00000

  0,00000

0,00000

0,00000

1

4,75918

   - 6,61945

- 3,66783

0,89909

4,77823

2

2,17319

   - 6,98914

- 3,98600

0,99280

4,98749

3

2,00881

   - 6,99976

- 3,99922

0,99964

4,99932

4

2,00048

   - 6,99998

- 3,99996

0,99998

4,99996

5

2,00003

   - 7,00000

- 4,00000

1,00000

5,00000

c нач. условиями X(I)=BET(I), I=1,N

K

X(1)

X(2)

X(3)

X(4)

X(5)

0

4,75918

   - 6,61945

- 3,66525

0,95925

5,00000

1

2,09493

   - 6,99887

- 4,00069

0,99500

4,99566

2

2,00207

   - 7,00049

- 3,99975

0,99992

4,99978

3

2,00015

   - 6,99999

- 3,99999

0,99999

4,99999

МЕТОД ГАУССА:

2,00000

  - 7,00000

- 4,00000

1,00000

5,00000
Скачать файл