Основи кореляційно-регресійного аналізу: Методичні вказівки для вивчення теми курсів “Теорія ймовірностей та математична статистика”, “Економетріка” і “Математика для економістів”, страница 9

Обробка даних малої вибірки

Мета цього розділу – допомогти студенту засвоїти методику обробки даних малої вибірки, або коли спостереження наведені в декількох повтореннях, але є невелика кількість різноманітних варіантів.

Продовжуємо аналіз прикладу, що розбирався послідовно протягом попередніх чотирьох розділів. Суто формально ми зробили обробку наведених вище даних (див. табл. 1) і переконалися в існуванні тісного і значущого кореляційного зв'язку між обсягами прохідницьких робіт і собівартістю 1 т вугілля, що добувається, причому більш тісною виявилася спряжена  залежність  .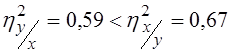

Як зазначалося вище, кореляційний аналіз не вирішує питання ані про природу досліджуваних зв’язків, ані про їхній напрямок – це справа фахівців. Але, на думку фахівців, між досліджуваними показниками взагалі не повинно бути ніяких зв’язків, тому що всі підготовчі роботи виконуються за рахунок капіталовкладень, і ці витрати не повинні враховуватися при розрахунку собівартості.

Як же пояснити отримані нами результати? (це є приклад змістовного аналізу, коли формальні статистичні процедури чергуються з неформальними висновками фахівців). Тут потрібне більш глибоке вивчення проблеми з урахуванням інших факторів, зокрема, мінливості даних за часом. Розглядаючи рис. 1  (продубльований  нижче на рис. 10), зауважимо, що залежності між x і y за кожний конкретний рік дійсно немає, проте з року в рік зростала собівартість вугілля, а в останні два роки істотно зростали також і обсяги прохідницьких робіт.

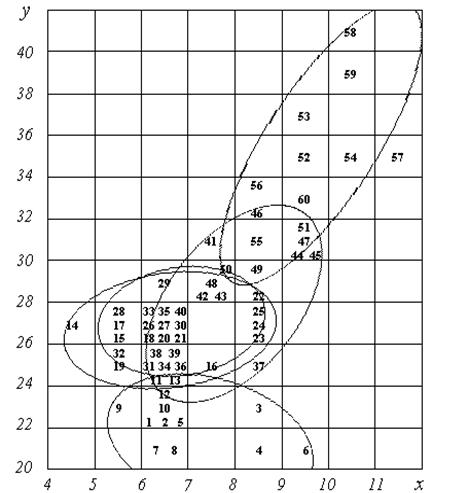
Рис. 10. Кореляційне поле

В останньому рядку табл. 1 наведені усереднені за кожний рік значення x і y.  Ці середньорічні дані виписані в табл. 8 (перші 4 стовпчика). Якщо ми маємо у своєму розпорядженні тільки ці середньорічні значення, то маємо справу з малої (n=5) вибіркою. Насправді в нас є 12–разова повторність кожного показника x і y, але в табл. 8 наведено не всі спостереження, а лише середні за групами (за кожний рік); цілком же вихідні дані містяться в табл. 1. Для того, щоб переходячи від табл. 1 до табл. 8 не втратити істотну інформацію про мінливість даних, необхідно крім середніх по групах обчислити і зберегти суми квадратів відхилень у кожній групі.

Таблиця 8

Обробка середньорічних даних

Розглянемо спочатку особливості обробки малої вибірки, вважаючи, що в табл. 8 наведені всі дані. Оскільки цих даних небагато (усього п’ять), жодних угруповань не потрібно. Іноді можна обійтися і без переходу до умовних одиниць, зокрема, у даному прикладі залишимо незмінними значення змінних x і y. Проте, щоб не мати справи з великими числами, із усіх значень  t  віднімемо середнє: T = t - 1983 (бажано так робити з усіма змінними; замість точних середніх можна віднімати найбільш близькі до середнього значення з таблиці, зокрема, зручно прийняти X = x – 7,9  і  Y = y – 28,7).