Основи кореляційно-регресійного аналізу: Методичні вказівки для вивчення теми курсів “Теорія ймовірностей та математична статистика”, “Економетріка” і “Математика для економістів”, страница 14

Безпосередньою підстановкою переконуємося, що розв’язком системи нормальних рівнянь є такі значення параметрів b₀ = 0,6245;  b₁ = 1,3057, що істотно відрізняються від параметрів породжуючої залежностіb₀ = b₁ = 1.

Розрахункові значення

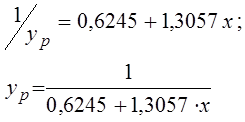
наведені в останніх двох стовпцях табл. 11, графіки ліній регресії зображені пунктирними лініями на рис. 13. При  х= 0  замість очікуваного значення h=1 (з похибкою порядку e =0,05) отримане  y_p=1,6 , що нікуди не годиться. Зовнішній вигляд графіка на рис. 13 б  і його розташування щодо емпіричних точок викликає сумніви в правильності вибору самої форми зв’язку.

Зробимо ж основний висновок з цього повчального прикладу: не можна відноситися до справи так, неначе метод найменших квадратів – сам по собі, а вихідні передумови – самі по собі. Пора усвідомити, що будь–які порушення вихідних гіпотез аналізу призводять до помилок у розв’язку, причому до помилок, які можна усунути шляхом деякої модернізації стандартної процедури оцінювання.

Для усунення гетероскедастичності помножимо обидві частини рівняння

Y = b₀ X₀ + b₁ X₁

на вагову функцію g. Форма зв’язку при цьому не зміниться. Вагову функцію підбираємо так, що б надійні спостереження з малим розкидом мали найбільшу вагу, а вплив викидів, по можливості, був виключений. Якщо ми бажаємо усунути погані наслідки функціонального перетворення результативної ознаки Y=F(y), то вагову функцію треба ввести так (нагадуємо, що  е = e^..F', де e – вихідні похибки):

g =1 / F'  .

Для нашого прикладу  F = 1 / y , F'= 1 / y² , g = y²  (знак не важливий).

Множимо обидві частини рівняння

1 / y = b₀ + b₁ x + e

на  g = y²  і одержуємо (e  = e×y²):

y = b₀ y² + b₁ xy² + e  .

Для цієї моделі (а модель – це не тільки форма зв’язку) система нормальних рівнянь має вигляд:

[y³] = b₀ [y⁴] + b₁ [x y⁴] ;

[x y³] = b₀ [x y⁴] + b₁ [x² y⁴] .

(умови ортогональності похибок до кожного члена моделі [e y²]=0,
[e x y²]=0 ). Необхідні суми підраховані в табл. 12, звідки одержуємо:

1,330 = b₀ ×1,284 + b₁×0,105 ;

0,298 = b₀ ×0,105 + b₁×0,209 .

Таблиця 12

Розрахунок сум з урахуванням вагової функції  g=y²

n	x	y	y3	y4	xy3	xy4	x2y4	1 / yp	yp	h
1	0	0,105	1,1576	1,2155	0	0	0	0,959	1,043	1
2	1	0,50	0,0911	0,0410	0,0911	0,0410	0,0410	1,901	0,526	0,5
3	2	0,383	0,0562	0,0215	0,1124	0,0430	0,0861	2,843	0,352	0,333
4	3	0,200	0,0080	0,0016	0,0240	0,480	0,0144	3,786	0,264	0,25
5	4	0,250	0,0156	0,0039	0,0624	0,0156	0,0624	4,728	0,212	0,2
6	5	0,117	0,0016	0,0002	0,0080	0,0010	0,0050	5,670	0,176	0167
Суми			1,3301	1,2837	0,2979	0,1054	0,2089

Розв’язком нової системи нормальних рівнянь є значення параметрів b₀ = 0,959,  b₁ = 0,942, що дуже близькі до очікуваних b₀ = b₁ = 1 (параметрів породжуючої залежності).

В останніх колонках табл. 12 обчислені розрахункові значення 1 / y_p і y_p ; для порівняння наведені ординати породжуючої залежності. Відповідність між заданою (h) і відновленої методом зважених НК залежностями дуже добра. Таким чином, заміна стандартної процедури МНК на більш загальну процедуру зважених НК забезпечила виконання передумови регресійного аналізу щодо рівноточності спостережень.