Основи кореляційно-регресійного аналізу: Методичні вказівки для вивчення теми курсів “Теорія ймовірностей та математична статистика”, “Економетріка” і “Математика для економістів”, страница 13

параметри якої легко оцінюються методом НК, для чого досить скласти і вирішити систему нормальних рівнянь. Однак помітимо, що після такого функціонального перетворення ми підмінюємо пошук мінімуму квадратів вихідних похибок [e² ] мінімізацією зовсім іншого функціонала  [e²] = [e²×(F'(y))²] . Неважко уявити ситуацію, коли множник F'(y) приймає істотно різні значення для різних спостережень, в результаті чого гомоскедастичність нев’язок моделі буде порушена.

Приведемо приклад наслідку порушення гомоскедастичністі, а також модифіковану процедуру МНК, призначену для подолання цих утруднень.

Нехай значення  у, що спостерігаються, породжуються точною залежністю 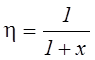 , на яку накладені похибки e = ±0,05 (тобто y = h(x) + e ); аргумент x  приймає послідовні цілі значення  0, 1, 2, 3, 4, 5, 6.

Чи можливо методом НК відновити аналітичний вид цієї формули за такими даними спостережень? Припускається, що форма зв’язку нам відома 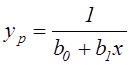 , таким чином, мова йде тільки про оцінку параметрів b₀ і b₁ , значення яких повинні бути близькими до одиниці (як було прийнято в породжуючій залежності).

Після функціонального перетворення Y=1/y модель формально стає лінійною

Y_p = b₀ + b₁ x

У табл. 10 і на рис. 13  наведені вихідні дані (x, h, e, y), перетворені значення результативної ознаки (1/h, 1/y) і нова система похибок  (e = 1/h ‑ 1/y) .

Таблиця 10

Вихідні і перетворені дані

n	x	h	e	y	1/h	1/y	e
1	0	1	0,05	1,050	1	0,952	‑0,048
2	1	0,5	‑0,05	0,450	2	2,222	0,222
3	2	0,333	0,05	0,383	3	2,611	‑0,389
4	3	0,25	‑0,05	0,200	4	5	1
5	4	0,2	0,05	0,250	5	4	‑1
6	5	0,167	‑0,05	0,117	6	8,547	2,547

Вже з цієї таблиці можна побачити “розбовтування” – збільшення розкиду перетворених даних із зростанням змінної х. На рис. 13 а це видно ще ясніше, причому остання точка  (x , ¹ /_y) навіть вийшла за поле графіка і схожа на викид. І, як і всякий викид, ця точка перетягнула в свій бік всю лінію регресії.

Наведемо всі викладки для розрахунку параметрів моделі

1 / y = b₀ + b₁ x + e .

Система нормальних рівнянь має вигляд:

[1 / y] = b₀ + b₁ [x] ;

[x / y] = b₀ [x]+ b₁ [x²] .

(умови ортогональності нев’язок до кожного члена моделі [e]=0, [ex]=0).

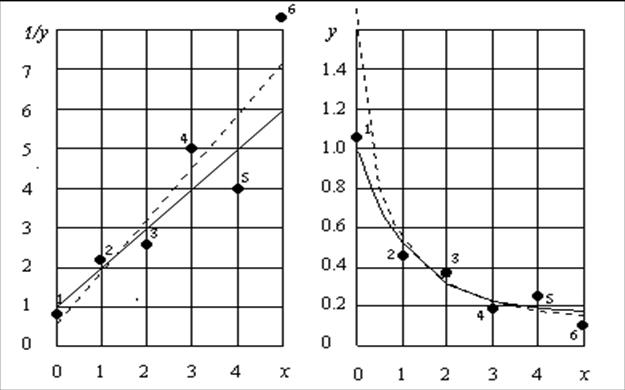
а                                                        б

Рис. 13 Нелінійна залежність у вихідних змінним (б)

і після функціональних перетворень (а)

емпіричні точки;

        Відновлена по МНК;

   Породжуюча залежність.

Усі необхідні суми підраховані в табл. 11, звідки одержуємо:

23,332 = b₀ ^. 6   + b₁ ^. 15 ;

81,179 = b₀ ^. 15 + b_1.55 _.

Таблиця 11

Розрахунок сум для МНК

n	x	x2	y	1 / y	х / y	1 / yp	yp
1	0	0	1,050	0,952	0	0,624	1,601
2	1	1	0,450	2,222	2,222	1,930	0,518
3	2	4	0,383	2,611	5,222	3,236	0,309
4	3	9	0,200	5,000	15,000	4,541	0,220
5	4	16	0,250	4,000	16,000	5,847	0,171
6	5	25	0,117	8,547	42,735	7153	0140
Суми	15	55		23,332	81,179