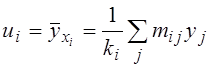 .
.
Нижче наведені обчислені за цією формулою координати вузлів емпіричної лінії регресії для нашого прикладу.
|
x = |
4,5; |
5,5; |
6,5; |
7,5; |
8,5; |
9,5; |
10,5; |
11,5 |
|
u = |
27,0; |
25,7; |
25,2; |
28,7; |
27,7; |
31,2; |
38,3; |
35,0 |
Розрахунки цих вузлів емпіричних ліній регресії будуть більш докладно наведені далі у загальній таблиці розрахунку сум (див. табл. 4).
При малому числі спостережень у деякі групи потрапляє занадто мало даних, тому середні значення показників у цих інтервалах будуть малонадійними. Емпірична лінія регресії в цьому випадку буде мати невиправдані зломи, “провали” чи “викиди”, які треба згладити. Рекомендується об’єднувати малонасичені інтервали з сусідніми доти, поки в кожному інтервалі буде не менш 5 спостережень, а для малої вибірки (n<100) – не менш 5% від загальної кількості спостережень, тобто не менш 0,05·n . Для нашого прикладу 0,05·60=3, тому об’єднанню підлягають крайні інтервали з частотами k1=k8=1. Для об’єднаних інтервалів треба обчислити обидві координати вузлів:
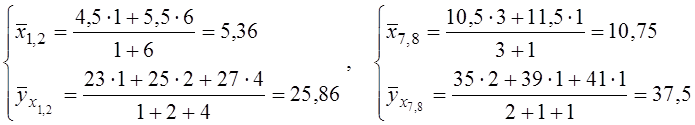 .
.
Точки з координатами (xi , ui) з’єднуємо відрізками прямих і одержуємо графік кореляційної залежності, навколо якого розсіяні вихідні точки (рис. 2).
У тих випадках, коли напрямок причинно-наслідкових зв’язків не відомий, обчислюють також вузли спряженої лінії регресії x по y (див. рис. 3), тобто середні значення показника x у кожній горизонтальній смузі табл. 2 :
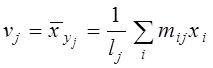 .
.
Малонасичені інтервали (9, 10, 11) об’єднуємо.
Зараз нам здається, що є єдиний можливий напрямок причинно-наслідкових зв’язків – від x до y , тобто зростання обсягів прохідницьких робіт може підвищувати собівартість продукції, але не навпаки; побудова ж спряженої залежності виправдано лише методичними міркуваннями, щоб показати, як це робиться в разі потреби. Однак не будемо квапитися з остаточними висновками. Кореляційний аналіз не вирішує питання ані про природу досліджуваних зв’язків, ані про їхній напрямок (“кореляція - не є причина”). Цілком можливо, що кореляція між двома змінними спостерігається лише тому, що обидва показники залежать від однієї і тієї ж самої причини. У такому випадку немає підстав підносити будь-який показник у ранг результативної ознаки і тим самим віддавати перевагу одній з спряжених залежностей; тут більш доцільним представляється використання “діагональної регресії”, графік якої збігається з головною віссю облака розсіювання. Спосіб побудови діагональної регресії буде поданий далі.
|
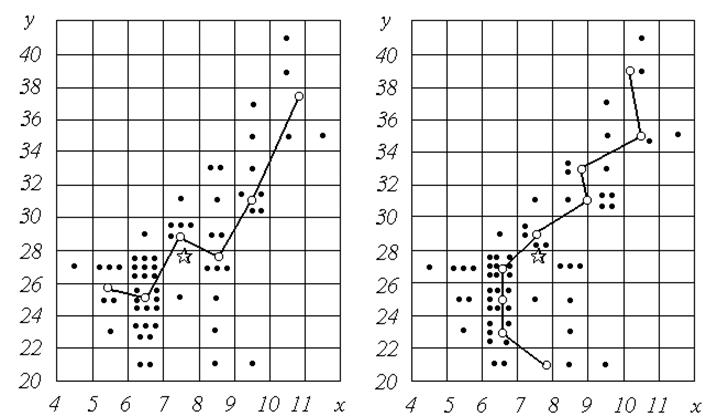
Рис. 2. Емпірична лінія |
Рис. 3. Емпірична лінія |
|
регресії y по x |
регресії x по y |
|
¶ – центр |
|
Наша мета – оцінити (обчислити) параметри лінійної моделі
y = b0 + b1 x + e .
Відомо, що ці параметри (коефіцієнти регресії) визначають за формулами:
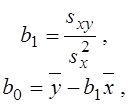
де 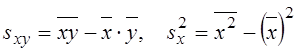 .
.
Отже,
нам потрібно підрахувати суми [x], [y], [x2],
[y2], [xy], де квадратними дужками позначено сумування
по всім спостереженням (позначення Гауса). У попередньому розділі дані були
піддані подвійному угрупованню (на kx=8 класів – по змінній
x і на ky= 11 класів – по змінний y). У
кореляційній табл. 2 приведені значення центрів класів, частоти mij
влучення емпіричних даних у клітинку з центром (xi ,
yj), сумарні частоти по стовпцях 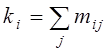 і рядках
і рядках 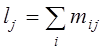 .
Загальне число спостережень
.
Загальне число спостережень 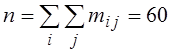 .
.
Розглянемо детально суми, що необхідні для розрахунку параметрів лінійної моделі, по згрупованих даних:
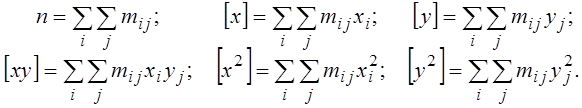
Першу суму можна обчислити по двох еквівалентних
формулах 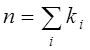 і
і 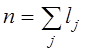 .
Подвійний розрахунок забезпечує надійний контроль. Для інших сум можна також
запропонувати обчислення з поточним контролем.
.
Подвійний розрахунок забезпечує надійний контроль. Для інших сум можна також
запропонувати обчислення з поточним контролем.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.