Основи кореляційно-регресійного аналізу: Методичні вказівки для вивчення теми курсів “Теорія ймовірностей та математична статистика”, “Економетріка” і “Математика для економістів”, страница 2

Так само робимо з іншою змінною: y_max=41,69 ; y_min=20,97 ; розмах D y=20,72 . При стандартної кількості класів k_y=10 крок дорівнює h_y=2,097 . Округляємо його до h_y=2 . Нові границі: y_max=42 ; y_min=20 ; D y=42 ‑ 20=22 . Нове число класів: k_y=Dy / h_y=11.

Будуємо сітку розміром 8 ´11. Тепер послідовно переглядаємо спостереження табл. 1 і наносимо відповідні точки на кореляційне поле. Особливої точності при нанесенні точок не потрібно, тому що дані, що попадають в одну клітинку, будуть округлені на її центр. Точки, що попадають на границю класів, треба відносити до інтервалу з більшим номером (є і прямо протилежна рекомендація, але вона не узгоджується з прийнятим у нас визначенням функції розподілу випадкової величини).

На рис. 1 приведене побудоване таким чином кореляційне поле, причому замість звичайних точок виявилося можливим (через невеликий обсяг вибірки) поставити номери спостережень, що подає додаткову інформацію до міркування: на малюнку можна виділити області розкиду даних за кожний рік. У подальшому аналізі ми використаємо цю додаткову інформацію: у даних за п'ятирічний період чітко проглядається кореляційна залежність – загальне облако розсіювання витягнуте по діагоналі і видно, що більшим обсягам прохідницьких робіт відповідають у середньому більші значення собівартості продукції.

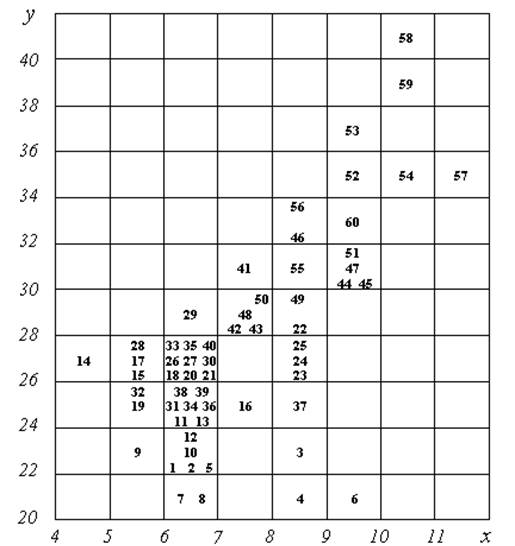
Рис. 1. Кореляційне поле

Підраховуємо на кореляційному полі кількість спостережень (частоти m_ij), що попадають у ту саму клітинку, і записуємо ці числа у відповідні клітинки табл. 2. Оскільки всі дані в одній клітинці осереднюються на її центр, у графах  x і y  табл. 2  наводимо лише їхні середні значення по групах. У остан­ньому рядку й в останньому стовпчику кореляційної таблиці обчислюємо суми частот по стовпцях і суми частот по рядках:

.

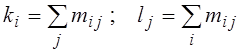Перший і останній рядки табл. 2 (рядки x, k) утворюють варіаційний ряд розподілу показника x; перший і останній стовпчики таблиці (стовпці y, l) – варіаційний ряд показника y; уся таблиця характеризує спільний розподіл двох показників  x, y. Будь-який стовпець таблиці містить частоти умовного розподілу показника  y  при фіксованому x; аналогічно, будь-який рядок таблиці містить частоти умовного розподілу показника  x  при фіксованому  y .

Таблиця 2

Кореляційна таблиця

Тепер ми можемо побудувати графік кореляційної залежності (графік емпіричної лінії регресії). Нагадуємо, що кореляційна залежність – це залежність центрів групування одного показника від значень іншого. Так, для розрахунку вузлів залежності  y  від  x  необхідно знайти всі “центри ваги” у вертикальних смугах табл. 2 (вважаючи частоти вагами) :