Основи кореляційно-регресійного аналізу: Методичні вказівки для вивчення теми курсів “Теорія ймовірностей та математична статистика”, “Економетріка” і “Математика для економістів”, страница 7

Індекс детермінації одержуємо шляхом ділення  SS_u   на  SS_y :

  .

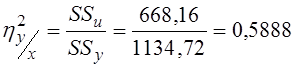Отриманий результат показує, що близько 59% мінливості  y  можна пояснити наявністю кореляційного зв’язку   y  по  x.

Для порівняння методик зробимо аналогічні статистичні висновки про значущість спряженого кореляційного зв’язку  x по y за готовими формулами без використання таблиці дисперсійного аналізу. Раніш при угрупованні даних на  l = 9  груп по змінній  y  були отримані такі значення оцінок дисперсій:

 .

Тут  v_j – середні інтервальні (середні групові).

Обчислимо індекс детермінації:

 .

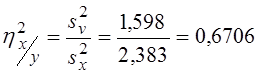Таким чином, спряженою кореляційною залежністю пояснюється 67% загальної мінливості  x , тобто спряжена залежність виявилася більш тісною.

Дисперсійне відношення Фішера

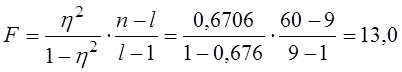
треба порівнювати з табличними значеннями F_0,05(8, 51)=2,10 і F_0,01(8, 51)= 2,82. Оскільки F=13,0 майже в 5 разів перевищує верхню межу F_0,01 , то “нуль-гіпотеза” відхиляється; спряжена кореляційна залежність визнається значущою.

Тіснота і значущість одновимірної лінійної моделі не залежить від напрямку причинно-наслідкових зв’язків. Для обох залежностей мірою тісноти зв’язку буде коефіцієнт кореляції:

 .

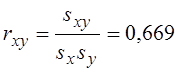Обчислюємо коефіцієнт детермінації:

(тобто близько 45% загальної мінливості пояснюється лінійним зв’язком).

Дисперсійне відношення Фішера:

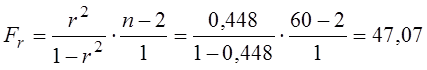
порівнюємо з табличними значеннями F_0,05(1, 58)=4  і  F_0,01(1, 58)=7. Оскільки F_r>F_0,01 , робимо висновок про значущість лінійної моделі.

Наведемо також таблицю дисперсійного аналізу (II) для перевірки значущості лінійної моделі (y по x). Нижній рядок нової таблиці (для загальної мінливості) такий же, як у табл. 5. Суми квадратів  SS_p  і  SS_e  обчислюємо за допомогою коефіцієнта детермінації   :

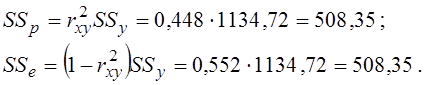
ЧСС залишків моделі дорівнює  n_e = n - 2 = 60 - 2 = 58, оскільки на залишки накладено два зв’язки – два рівняння нормальної системи; останнє ЧСС одержуємо як різницю:  n_p = n_y - n_p = 59 – 5 = 1.

Таблиця 6

Дисперсійний аналіз (II)
для перевірки значущості лінійної моделі

Інші елементи табл. 6 – такі самі, як і для табл. 5.

За таблицею дисперсійного аналізу отримано попереднє значення дисперсійного відношення F_r = 47,07, і зроблений той самий висновок про значущість моделі, що і при використанні готової формули.

Отже, встановлено факт наявності значущого кореляційного зв’язку  y по x, що пояснює 58,9% усієї мінливості результативної ознаки. Для опису цього зв’язку прийнято лінійну модель. Вона також виявилася значущою, але пояснила лише 44,8% повної мінливості. Різниця (h² ‑ r²)´100% = 58,9 – 44,8 = 14,1%  обумовлюється систематичними похибками (похибками специфікації, неадекватністю моделі).

Чи істотний цей чи ефект, чи не можна ним знехтувати?  Перевірку адекватності лінійної моделі також робимо в таблиці дисперсійного аналізу.

Таблиця 7

Дисперсійний аналіз (III)
для перевірки адекватності лінійної моделі.