Основи кореляційно-регресійного аналізу: Методичні вказівки для вивчення теми курсів “Теорія ймовірностей та математична статистика”, “Економетріка” і “Математика для економістів”, страница 5

Графіки емпіричних ліній регресії приведені на рис. 2, 3. Зауважимо, що вузли емпіричних ліній регресії є центри відповідних класів (вертикальних або горизонтальних смуг). Облако розсіювання точок витягнуте вздовж деякої осі (діагональної регресії). Спосіб побудови діагональної регресії буде описаний у наступних розділах. Візуально переконуємося, що більшим значенням однієї змінної, як правило, відповідають більші значення іншої змінної.

Розрахунок параметрів лінійної моделі

Продовжуємо розрахунки параметрів лінійної моделі. З табл. 4 виписуємо обчислені суми (в умовних змінних):

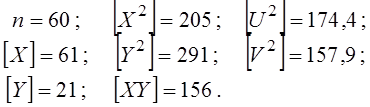
Ділимо ці суми на   n=60  і одержуємо середні:

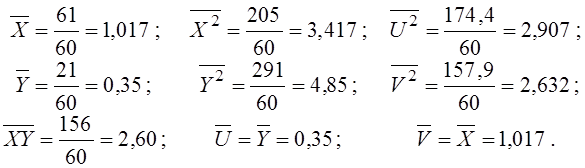
Тепер обчислюємо дисперсії (за формулою “середній квадрат” мінус “квадрат середнього”) і коваріацію (за формулою “середній добуток” мінус “добуток середніх”):

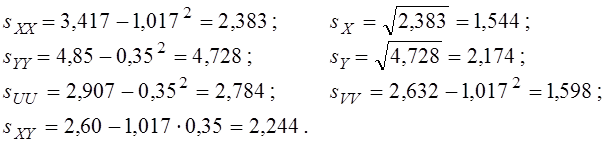
Робимо зворотний перехід до вихідних змінних:

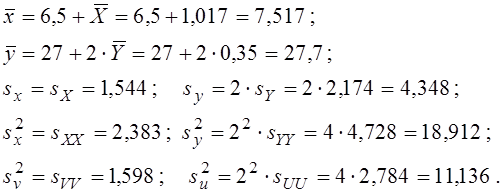
Коефіцієнт кореляції – величина безрозмірна і не змінюється при переході до реальних змінних:

 .

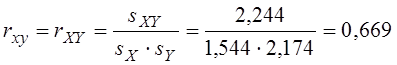Угруповання даних дозволило досить просто виконати вищенаведені розрахунки, однак при цьому було припущено деяких похибок, оскільки дані, що попадають в одну клітинку, осереднювались на її центр. Для оцінки похибок угрупувань за вихідними даними цього ж прикладу були зроблені розрахунки на ЕОМ (без угрупувань). Порівняємо отримані результати:

Будемо мати на увазі, що подвійне угрупування даних по сітці порядку 10´10 призводить приблизно до 5%-вої похибки.

Тепер обчислюємо коефіцієнти регресії  y  по  x :

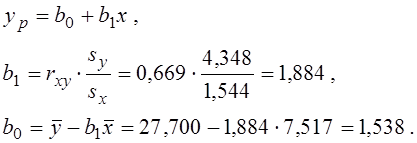
Отримано рівняння регресії (рівняння кореляційної залежності)

y_p = 13,538 + 1,884 x .

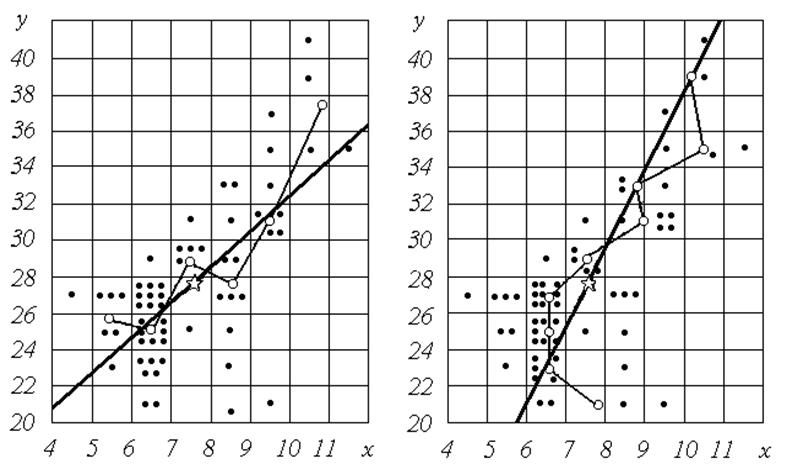
Графік цієї лінії наведений на рис. 4 разом із графіком відповідної емпіричної залежності. Зауважимо, що вузли емпіричної лінії групуються навколо лінії регресії.

Для прикладу обчислимо параметри спряженої залежності:

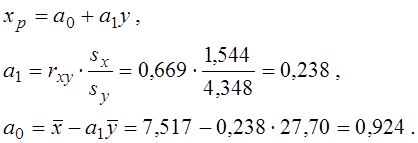
Графік спряженої залежності наведений на рис.5 разом із графіком відповідної емпіричної лінії регресії.

Нарешті розрахуємо параметри діагональної “регресії”:

 ,

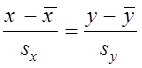чи                                                                                y = c₀ + c₁ x ,  

де 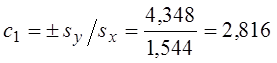                (знак  ±  вибирається за знаком r_xy),

 .

Графік діагональної регресії наведений на рис. 6; ця лінія збігається з головною віссю облака розсіювання емпіричних точок.

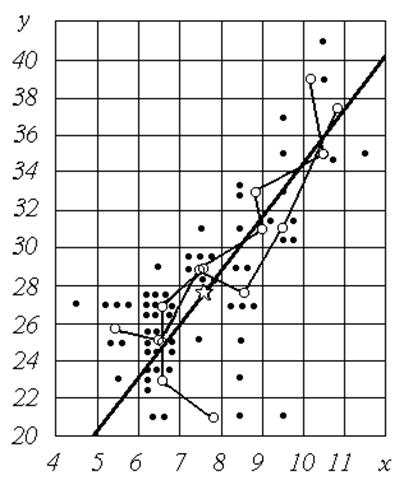
Рис. 6 Діагональна й емпіричні лінії регресії

Дисперсійний аналіз

Мета цього розділу – зробити всі статистичні висновки після формальної оцінки параметрів моделі і дисперсії залишку. Передусім варто перевірити значущість і адекватність моделі, для чого існують готові формули. Розглянемо послідовність викладок дисперсійного аналізу в табличній формі, оскільки деякі програми статистичного аналізу (наприклад, відомий ППП Статграф) видають результати саме так.

Таблиці дисперсійного аналізу (одновимірного дисперсійного аналізу) уніфіковані, мають однакові графи і заголовки. Нижче, для нашого прикладу, що аналізується послідовно, наведена таблиця дисперсійного аналізу I для перевірки значущості кореляційного зв’язку y по x (табл. 5). Розглянемо детально всі елементи цієї таблиці.

У цьому прикладі наявні дані (60 спостережень) були згруповані на 6 класів за різними значеннями аргументу x. Тепер ці дані можна представити таким чином

y_ij = u_i + e _ij ,

де y_ij  - значення, що спостерігаються (“повний сигнал”); u_i – середні по групах (“корисний сигнал”); e _ij – випадкові похибки (“шум”).