Основи кореляційно-регресійного аналізу: Методичні вказівки для вивчення теми курсів “Теорія ймовірностей та математична статистика”, “Економетріка” і “Математика для економістів”, страница 4

Оскільки від зміни порядку підсумовування подвійні суми не змінюються, то для їх розрахунку можна запропонувати два способи підсумовування.

Наприклад, для третьої суми:

  .

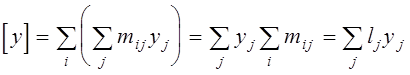                                   (перший спосіб)     (другий спосіб)

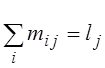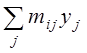Тут при заміні порядку підсумовування вдалося винести за знак першої суми  y_i  і замінити . При першому способі треба попередньо обчислити проміжні суми , а потім їх усі скласти. Цей, більш громіздкий, спосіб виправданий тим, що всі проміжні суми 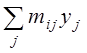 будуть потрібні ще мінімум два рази. Нагадаємо, що ординати вузлів емпіричної лінії регресії   виражаються через ці суми:  .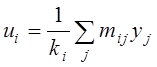

Аналогічно:      .

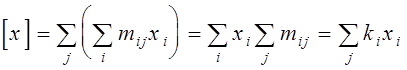Абсциси спряженої лінії регресії 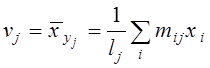  виражаються через проміжні суми  .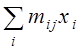

Далі:            .

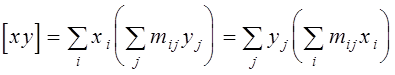 (перший спосіб)    (другий спосіб)

Тут третій раз використовуються проміжні суми 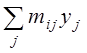  і  .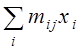

Для наступних двох сум (сум квадратів) виправданий лише один спосіб підсумовування:

.

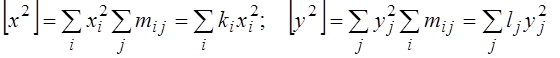Для контролю пропонується обчислити по цих же формулах допоміжні суми  [(x±1)²]  і  [(y±1)²] . Контроль полягає у тому, що ці суми можуть бути виражені через попередні:

[(x±1)²] = [x²] ± 2 [x] + n ;   [(y±1)²] = [y²] ± 2 [y] + n .

Тут знак  +  чи  ‑  обирають довільно (наприклад, з метою зробити допоміжні суми як найменше).

Для дисперсійного аналізу будуть потрібні ще такі суми: [u], [v], [u²], [v²].

Перші дві суми виражаються через раніше введені:

 .

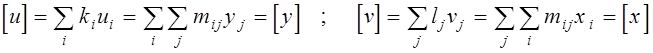Дві суми, що залишилися, підраховуємо одним способом:

  .

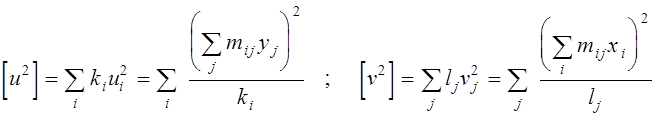От і вчетверте використані проміжні суми.

Для контролю можна обчислити допоміжні суми :

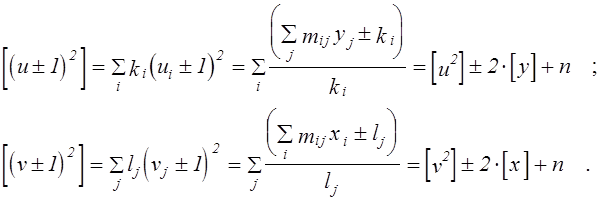
При розрахунку ординат (і абсцис для спряженої моделі) вузлів емпіричних ліній регресії  u_i , v_j  не слід забувати про необхідність укрупнення малонасичених інтервалів, у які потрапило менше 5% усіх спостережень (для малої вибірки) чи менше 5-ти спостережень (для великої вибірки). У нашому випадку 5% від  n=60  буде 3. Об’єднувати доведеться крайні інтервали.

Оскільки дані згруповані в інтервали однакової довжини, то доцільно зробити перехід до безрозмірних змінних :

   .

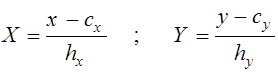Тут  h_x , h_y - крок угруповань, а  c_x , c_y  – середини центральних найбільш насичених інтервалів, які, на на перший погляд, близькі до середнього   .

У нашому випадку h_x = 1 , .k_max= k₃ = 24 , тому обираємо c_x = 6,5. За іншою змінною  h_y = 2 , .l_max= l₄ = 16 ,  тому обираємо  c_y = 27 .

Отже,   .

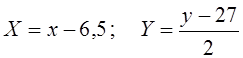Тепер центри груп по X  будуть цілими числами від  ‑2 до 5, а по Y  від ‑3 до 7. Більшість сум, що обчислюються, (крім [u²] і [v²]) будуть в умовних змінних цілочисловими. Окрім істотного спрощення усіх викладок, перехід до умовних змінних підвищує точність розрахунків, і тому цей перехід бажаний, навіть якщо дані не згруповані.

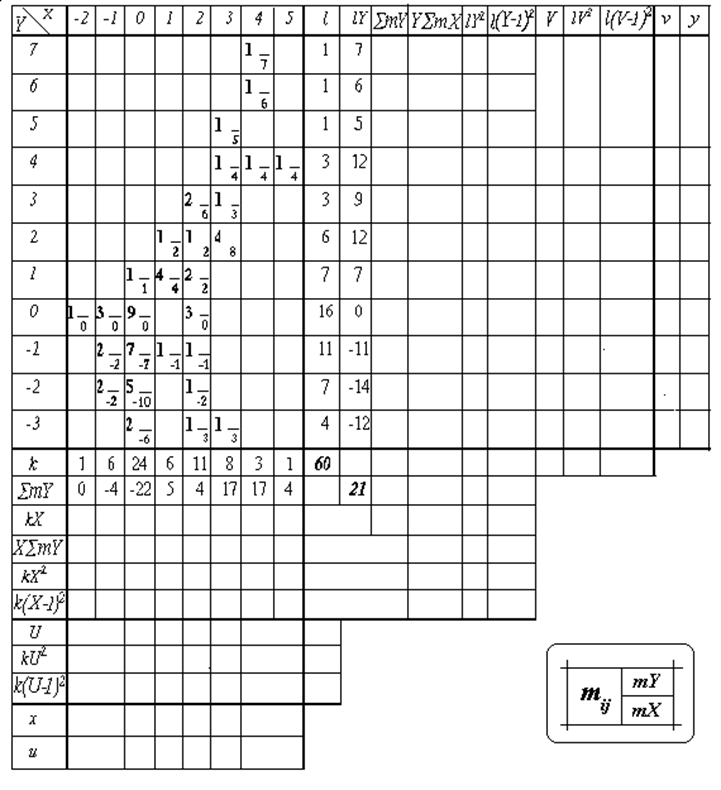
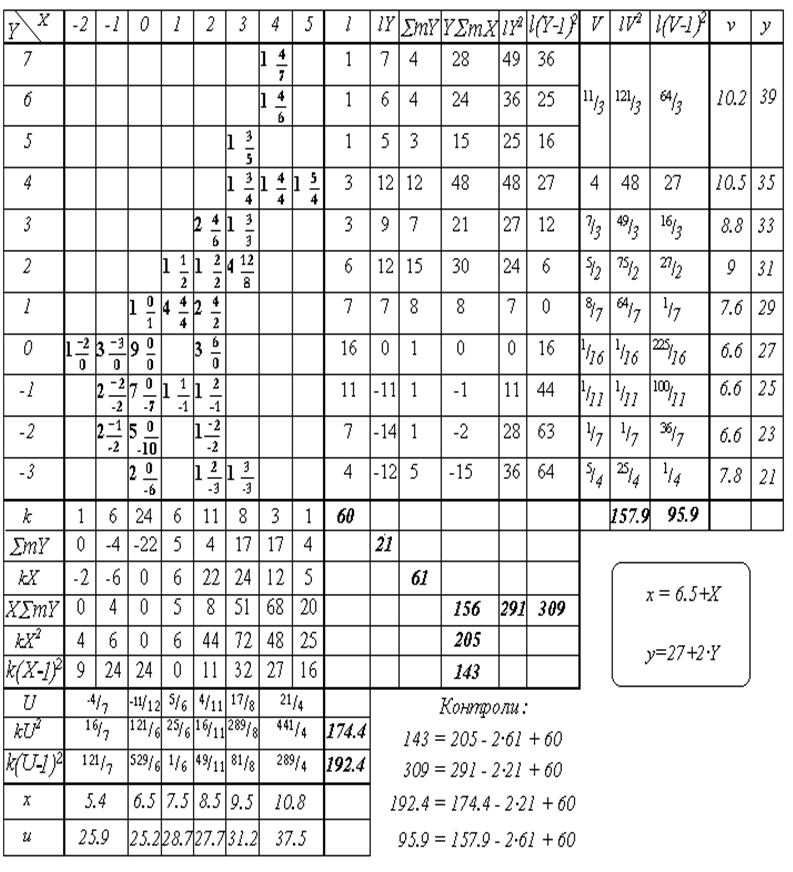
Для розрахунку сум пропонується спеціальна форма таблиці, яка, не зважаючи на досить громіздкий вигляд, дуже зручна. Центральна частина таблиці розрахунку сум (табл. 3, 4) містить цілком кореляційну таблицю (табл. 2), але центри класів тепер наведені вже в умовних змінних. Кожна клітинка центральної частини табл. 3 поділена на 3 поля, де ліворуч записуються частоти  m_ij, праворуч зверху – добутки m_ij X_i  і праворуч знизу – добутки m_ijY_j . Фрагмент заповнення таблиці розрахунку сум приведений у табл. 3, повністю заповнена таблиця – у табл. 4. Основна частина таблиці розрахунку сум суміщена з двома додатковими таблицями знизу і праворуч. У цих додаткових таблицях розраховуються координати вузлів емпіричних ліній регресії і обчислюються суми квадратів для наступного розрахунку дисперсії цих вузлів. В останніх двох рядках (останніх двох стовпчиках) наведені координати вузлів емпіричних ліній регресії в реальних вихідних змінних.

Зворотний перехід виконується за формулами:

  .

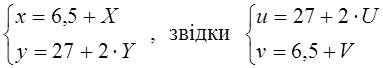Таблиця 3

Фрагмент таблиці розрахунку сум

Таблиця 4

Заповнена таблиця розрахунку сум