Основи кореляційно-регресійного аналізу: Методичні вказівки для вивчення теми курсів “Теорія ймовірностей та математична статистика”, “Економетріка” і “Математика для економістів”, страница 10

Знайдемо лінійні кореляційні залежності показників  x  і  y  від часу  t .

У підсумковому рядку табл. 8 розраховані середні:

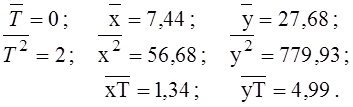
Обчислюємо дисперсії і коваріації:

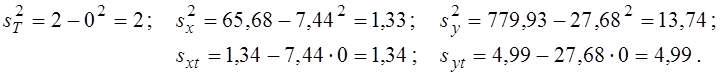
Далі обчислюємо коефіцієнти регресії і коефіцієнти кореляції для обох тимчасових залежностей:

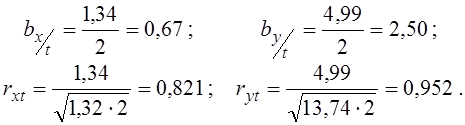
По усередненим даним отримані дуже високі значення коефіцієнтів кореляції, явно завищені. Так завжди буває, оскільки при усередненні по групах губиться випадкова мінливість. Проте за даними малої вибірки не будемо робити далекоглядних висновків ані про тісноту, ані про значущість кореляційних зв'язків. Винятково з навчальною метою обчислимо дисперсійні відношення Фішера і порівняємо їх з табличними значеннями:

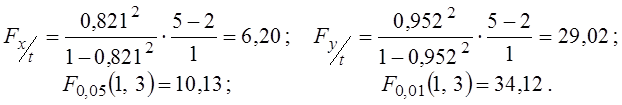
Незважаючи на високі (явно завищені) значення коефіцієнтів кореляції, жодна з отриманих кореляційних зв’язків не визнана значущою (перша залежність незначуща, тому що  ; значущість другої залежності залишена під сумнівом, тому що обчислене дисперсійне відношення потрапило в область невизначеності критерію ).

Виписуємо рівняння регресії:

  .

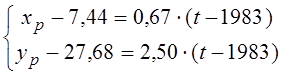Графіки обох залежностей наведено на рис. 11.

Якщо тепер виключити параметр t, то вийде лінійна залежність між показниками x і y:

 

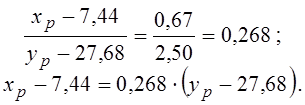
Графік цієї параметричної залежності дуже близький до спряженої  лінії регресії x по y:

 .

Невеличка різниця між усіма параметрами цих двох моделей може бути пояснена тим, що параметри спряженої залежності були отримані з згрупованими даними. Графік спряженої лінії регресії зображений на рис. 11 пунктиром.

Отже, знайдена кореляційна залежність x від y пояснюється впливом загальної причини (це є хибна кореляція).

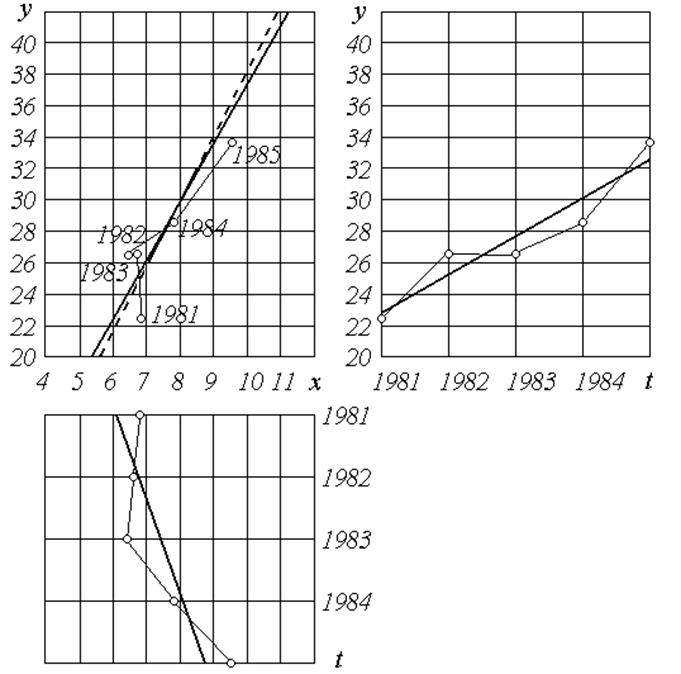
Рис. 11 Тимчасові залежності x-t, y-t і параметрична залежність x-y
(пунктир - лінія регресії x по y)

Аналіз господарської діяльності на цьому, природно, не закінчується. Виникає закономірне питання: а чому щороку підвищувалося собівартість продукції? Очевидно, через недостатній обсяг проведених підготовчих робіт з кожним роком знижувалося добування вугілля, що і призводило до збільшення його собівартості. Водночас з цим форсувалися роботи по підготовці горизонтів до експлуатації. Для підтвердження цього висновку потрібно залучити додаткові дані про обсяги видобутку вугілля за кожний рік.

А тепер врахуємо, що фактично ми маємо справу з досить великою вибір­кою (n=60), але дані угруповані на невелике число рівнонасичених груп (5 років по 12 спостережень). Для оцінки параметрів моделей обробляємо середньорічні значення так само, наче ми маємо справу з малою вибіркою. Проте при оцінці тісноти, значущості та адекватності моделі треба враховувати вже всі вихідні дані. Перерахуванню підлягають оцінки дисперсій  ; при ручному розрахунку доведеться дані групувати, але групувати окремо на k інтервалів по  x  і (окремо) на  l  інтервалів по  y (подвійного угруповання не потрібно). Ці дисперсії вже були обчислені нами раніше (по згрупованим даним):

 .

У дужках для порівняння наведені дисперсії середньорічних значень (дисперсії вузлів емпіричних ліній регресії), і більш правильним тут була би зміна позначень:

 ,

де                v_j – середньорічні значення x;

u_i – середньорічні значення y.

Коваріації   s_xt=1,34  і  s_yt=4,99  не зміняться.

Обчислюємо індекси детермінації:

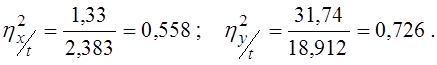
Перераховуємо коефіцієнти кореляції і коефіцієнти детермінації:

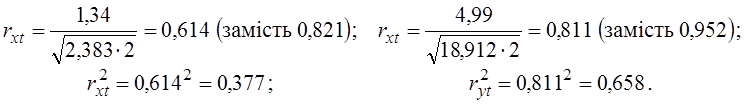
Отже, кореляційною залежністю x від t пояснюється 55,8% мінливості x, лінійна модель пояснює лише 37,7% ; кореляційною залежністю y від t пояснюється 81,1% мінливості  y, лінійна модель пояснює лише 65,8% .

Перевіряємо значущість існуючих кореляційних зв’язків за критерієм Фішера (дисперсійний аналіз I):

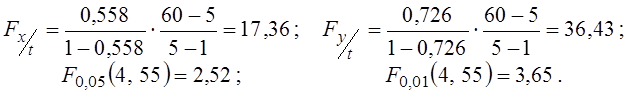
Обидві залежності від   t  - значущі, тому що   .

Перевіряємо значущість лінійних моделей (дисперсійний аналіз II):

 

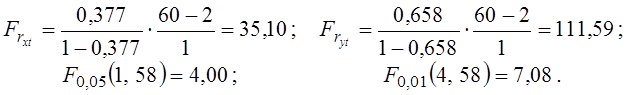
Обидві лінійні моделі виявилися значущими, тому що  F_r > F_{0,01 .}

Помітимо, що за даним лише малої вибірки жодна з цих моделей не була визнана значущої.