Основи кореляційно-регресійного аналізу: Методичні вказівки для вивчення теми курсів “Теорія ймовірностей та математична статистика”, “Економетріка” і “Математика для економістів”, страница 8

Два нижніх рядки табл. 7 узяті з інших таблиць дисперсійного аналізу (табл. 5 і табл. 6); у рядку, що залишився, для систематичної помилки обчислюється сума квадратів і ЧСС як різниці відповідних елементів уже відомих рядків. Отримане значення дисперсійного відношення F_A=4,62 тут перевищує верхню межу F_0,01=3,65; отже лінійна модель не може бути визнана адекватної.

Перевірку адекватності спряженої моделі зробимо, навпаки, за готовою формулою (для порівняння методик):

  .

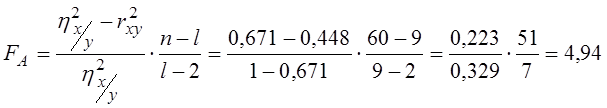Тут: l=9 – число груп за змінною y;

h²‑ r²=0,223 означає, що 22,3% мінливості результативної ознаки x не пояснюється лінійною моделлю (з  67,1% пояснене 44,8%).

Величина F=4,94 означає, що мінливість “шкідливого сигналу” (систематичної помилки) майже в 5 разів перевищує мінливість випадкової перешкоди. Отримане значення порівнюємо з табличними значеннями  F_0,05(7, 51)= 2,26 ;  F_0,01(7, 51)=3,14. Лінійна модель для опису залежності  x по y  також виявилася неадекватною, оскільки  F_A=4,94>F_0,01 .

Дійсно, розглянемо поведінку вузлів емпіричних ліній регресії на рис 2 і 3 (чи на рис. 4 і 5). Візуально відзначаємо, що ці вузли явно групуються навколо деяких кривих (особливо це виявляється для спряженої залежності). У всякому разі, лінійна модель при будь-якому виборі її параметрів не в змозі описати особливості цих емпіричних ліній. Тут варто перейти до більш складної фор­ми зв’язку, наприклад, до квадратичної моделі.

На завершення побудуємо межі 95%-вої довірчої смуги  (смуги невизначеності) на лінії регресії. Розглянемо спрощений спосіб побудови границь цієї довірчої смуги  y_p ±D y_p ,  де

 .

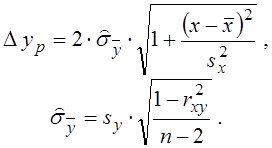Цей вираз із заміною позначень є рівнянням спряженої гіперболи:

 ,

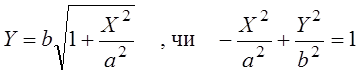де      –  нові змінні;

a, b – півосі гіперболи:   .

Графік спряженої гіперболи зображено на рис. 7. Відзначимо такі особливості цього графіку: ширина гіперболічної смуги на інтервалі [‑ a, a] приблизно однакова і дорівнює  ±b; далі границі смуги помітно розширюються, наближаючись до лінійних асимптот 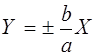  – продовженням діагоналей прямокутника зі сторонами (±a, ±b).

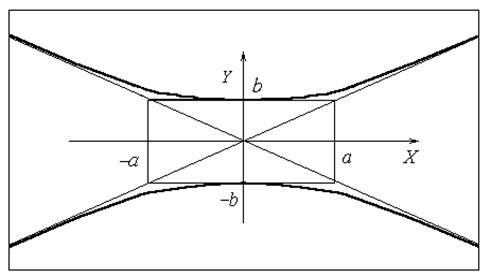
Рис. 7.  Графік спряженої гіперболи

У реальних змінних (x, y) саме вузьке місце смуги зсунуте вправо на  (з урахуванням знаку) і смуга витягнута вздовж лінії регресії. На інтервалі  величина довірчої похибки ±D y_p практично постійна і дорівнює 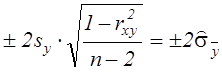. Наносимо ці постійні границі на графік y_p = b₀ + b₁ x . Одержуємо паралелограм зі сторонами . У цьому паралелограмі проводимо діагоналі і продовжуємо їх за його межі. Продовження діагоналей і є границями 95%-ної довірчої смуги для  .

У нашому прикладі  s_x=1,544;   s_y=4,348;  r_xy=0,669;  n=60  .

Обчислюємо:              .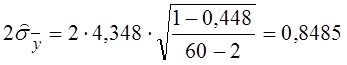

Цю величину можна також обчислити за формулою:

 ,

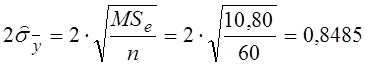де    беремо з табл. 6.

На рис. 8  довірча смуга побудована викладеним вище спрощеним способом. Аналогічно, на рис. 9  побудовано довірчу смугу на спряжену лінію регресії: вона зберігає приблизно однакову ширину на інтервалі , яка дорівнює 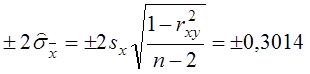; далі межі смуги наближаються до діагоналей побудованого паралелограма.

Наявність довірчої смуги дозволяє визначити межі застосування моделі. У всякому разі, кореляційні моделі явно непридатні для прогнозування в сенсі екстраполяції за межі облака розсіювання спостережуваних точок. Найбільш надійні результати (з малою довірчою похибкою) будуть в околі центра угруповання даних , далі довірча похибка швидко збільшується. Довірча смуга – це область невизначеності зроблених статистичних висновків. Будь-яка залежність, графік якої цілком розміщується в довірчій смузі, є конкуруючою моделлю відносно прийнятої, параметри якої розраховані за МНК –даних недостатньо, щоб упевнено зробити вибір між цими конкуруючими моделями. Зокрема, за незначущості кореляційної моделі в її довірчій смузі цілком розміщується горизонтальна пряма, графік якої показує незмінність середніх значень результативної ознаки при будь-яких значеннях змінної-аргументу.