Задача №2. Лётчик катапультировался над местностью, 60% которой занято лесом, 40% – поля. Вероятность успешного приземления парашютиста в лесу равна 0.3, а в поле – 0,9. Найти вероятность того, что лётчик приземлится благополучно.
Задача №3. Датчик контроля нагрева букс с вероятностью 0,6 может принадлежать к первому типу, с вероятностью 0,3 – ко второму типу и с вероятностью 0,1 – к третьему типу. Вероятность обнаружения перегрева буксы датчиками каждого типа соответственно равны 0,95; 0,91; 0,8. Какова вероятность того, перегрев буксы будет обнаружен?
Задача №4. Электронное устройство может эксплуатироваться в трёх различных режимах, причём в первом режиме – с вероятностью 0.5, во втором – с вероятностью 0,4. При функционировании устройства в первом режиме его отказ (в течение нормативной наработки) может возникнуть с вероятностью 0.05, во 2-м режиме – с вероятностью 0.1, в третьем режиме – с вероятностью 0,15. Найти вероятность того, что в течение нормативной наработки в устройстве возникнет отказ.
Задача №5. При передаче сообщения сигналами «точка» и «тире» эти сигналы встречаются в соотношении 5:3. Под действием помех искажаются в среднем 1/5 сигналов «точка» и 2/11 сигналов «тире». Найти вероятность того, что некоторый принятый сигнал не искажен.
Задача №6.
На рисунке изображена схема дорог.
Туристы вышли из пункта O, выбирая наугад на разветвлении дорог один из
возможных путей. Какова вероятность того, что они попадут в пункт A? 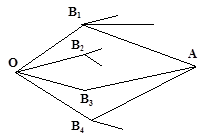
Задача №7. В коробку, содержащую 4 реле, добавлено неисправное реле. Какова вероятность извлечения исправного реле, если все предположения о первоначальном числе неисправных реле равновозможны.
Задача №8. Для зачета по дисциплине, включающей три раздела, студенту осталось ответить на дополнительный вопрос. Преподаватель может задать вопрос по первому и второму разделу с вероятностями ¼, по третьему разделу – с вероятностью ½. С какой вероятностью студент получит зачёт, если по первому разделу студент подготовил 90 вопросов из 100, по второму разделу – 50 из 75-ти, по третьему разделу студент подготовил все 80 вопросов?
Задача №9. Последовательно послано 4 радиосигнала. Вероятности приема каждого из них не зависят от того, приняты ли остальные сигналы, и соответственно равны 0.1, 0.2, 0.3 и 0.4. Определить вероятность установления двусторонней связи, если вероятность этого события при приеме одного сигнала равна 0.2, при приеме двух сигналов – равна 0.6, а при приеме трех и четырех сигналов – единице.
Задача №10. Сообщение может передаваться по одному из каналов связи, находящихся в различных состояниях: из них n1 каналов находятся в отличном состоянии, n2 – в хорошем, n3 – в посредственном, и n4 – в плохом. Вероятность правильной передачи сообщения для каналов разного вида равна, соответственно p1, p2, p3, p4. Для повышения его достоверности сообщение передается два раза по одному и тому же каналу, который выбирается наугад. Найти вероятность того, что хотя бы один раз оно будет передано правильно.
Задача №11. Студент подготовил лишь 25 билетов из 30. Каким по счёту он должен сдавать экзамен, чтобы вероятность вытянуть неизвестный билет была бы для него минимальной?
Задача №12. Вероятность диагностирования (обращения к врачу дольного) туберкулёза на ранней стадии – 0,5; на второй стадии – 0,4; на последней стадии – 0,1. Вероятность успешного лечения болезни на ранней стадии равна 0,99; на второй стадии – 0,6; на третьей стадии – 0,2. Найти вероятность того, что при диагностировании туберкулёза у случайного человека (на некоторой стадии), он будет вылечен.
Задача №13. В урне находятся четыре шара, каждый из которых может оказаться либо белым, либо черным. Все варианты состава шаров предполагаются равновозможными.
a) Найти вероятность того, что при случайном вынимании из урны появится белый шар.
b) При выборе из урны появился белый шар. Какова вероятность того, что следующий вынутый из урны шар также окажется белым?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.