h)
![]() .
.
Задача №9. Внутри прямоугольника, изображенного на рисунке 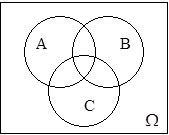 , выбирается наугад точка.
Определены следующие события:
, выбирается наугад точка.
Определены следующие события:
A={выбранная точка принадлежит кругу A};
B={выбранная точка принадлежит кругу B};
C={выбранная точка принадлежит кругу C}.
Заштриховать области элементарных исходов, благоприятных следующим случайным
событиям: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Задача №10. Установите, какие из следующих утверждений истинны:
a)
![]() ;
;
b)
![]()
c)
![]() ;
;
d)
![]() ;
;
e)
![]() ;
;
f)
![]() ;
;
g)
![]() ;
;
h)
![]() ;
;
i)
![]() ;
;
j)
![]() .
.
Задача №11. Доказать, что для произвольных событий A и B,
событие ![]() является достоверным, а событие
является достоверным, а событие ![]() – невозможным.
– невозможным.
Практическое занятие №2
Тема: «Классический способ вычисления вероятностей случайных событий. Формулы комбинаторики»
План:
§ Повторение лекционного материала;
§ Проверка отсутствующих;
§ Решение задач;
§ Проверка домашнего задания, в том числе задач РГР;
§ Выдача нового домашнего задания.
Задачи для решения
Задача №1. В коробке находятся 10 транзисторов, три из которых неисправны. С какой вероятностью для сборки однокаскадного усилителя будет выбран исправный транзистор?
Задача №2. Игральная кость подбрасывается два раза. Найти
вероятности следующих событий:
A={при обоих подбрасываниях выпадет одинаковое число очков};
B={при первом подбрасывании выпадет большее число очков, чем при
втором}.
Задача №3. (Задача де Мере) Какая сумма очков имеет больше шансов выпасть при бросании двух игральных костей – 11 или 12?
Задача №4. Сколько всего может быть получено карт с пятью номерами: 6, 7, 8, 9, 10 и четырьмя мастями: §,¨,©,ª? (_20)
Задача №5. Сколько комбинаций чисел может быть получено при бросании трех костей? (_216)
Задача №6. Сколько возможно вариантов паролей для доступа к данным Internet сервера, если пароль содержит
a) ровно 5 цифр;
b) не более 5 цифр;
c) ровно 5 символов (включая цифры и 26 букв латинского алфавита);
d) не более 5 символов (включая цифры и 26 букв латинского алфавита).
Задача №7. На сортировочном пути без подборки в ожидании подачи стоят 6 вагонов. Определить вероятность того, что вагоны стоят в нужном для подачи порядке.
Задача №8. В распределительном шкафу три различных потребителя
энергии (a, b, c) подключаются к трехфазной сети переменного тока. К
каждой фазе подключается только один потребитель. 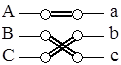
a) Сколько возможно вариантов подключения потребителей к фазам переменного тока?
b) С какой вероятностью потребители будут подключены к фазам в соответствии с рисунком, если электромонтер выполняет соединение случайным образом?
c) С какой вероятностью потребитель «b» будет подключен к фазе «B»?
Задача №9. С какой вероятностью напряжение между двумя, выбранными наудачу, проводами трехфазной цепи переменного тока с нулевым проводом составит 380 В, если напряжение между фазными проводами 380 В, а между фазным и нулевым проводом 220 В?
Задача №10. В азбуке Морзе буквы представляются последовательностями тире и точек с возможными повторениями. Сколько букв можно составить из четырех символов?
Задача №11. На сортировочную станцию поступили по одному вагону из
трех городов: Орши, Могилева и Витебска. Предполагая все возможные варианты
очередности разгрузки этих трех вагонов равновозможными, найти вероятности
следующих событий:
A={вагон из Могилева будет разгружен не ранее, чем вагон из Витебска};
B={первым будет разгружен вагон из Орши}.
Задача №12. Сколько возможно вариантов PIN-кода кредитной пластиковой карты, если код состоит из четырех цифр?
Задача №13. Найти вероятность того, что злоумышленник с первой попытки получит деньги в банкомате по чужой карточке.
Задача №14. Камера хранения бассейна открывается при верном наборе кода из четырех символов. Первый символ – одна из 10 букв, оставшиеся символы кода – цифры: 0…9. С какой вероятностью злоумышленник в течение часа откроет камеру хранения, если на набор каждой комбинации он тратит в среднем 4 секунды? (_0,09)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.