Задачи к практическим занятиям № 1-7 по дисциплине "Высшая математика" (Случайные события. Пространство элементарных событий. Операции над событиями. Построение доверительных интервалов. Проверка параметрических гипотез), страница 15

Задача №5. Найти вероятность того, что случайная величина x примет значение, большее величины h, если каждая из них имеет показательный закон распределения со средними значениями M[x]=m₁ и M[h]=m₂ соответственно.

Задача №6. Если автобусы ходят строго через 10 минут, а мы подходим на остановку в произвольный момент времени, то в среднем нам придется ждать 5 минут. Если же интервалы между автобусами случайны со средним значением 10 минут, то нам в среднем придется ждать более 5 минут (иногда значительно). В частности, если интервал между автобусами имеет показательное распределение, то среднее время ожидания автобуса равно среднему времени интервала движения.

Пусть F(t) и f(t) функция и плотность интервала движения автобуса, где t измеряется от момента отправления последнего автобуса. Плотность вероятности ожидания равна  t*f(t)/m, т.к. вероятность нашего появления в течение некоторого времени пропорциональна его длине t. Таким образом, среднее время ожидания T вычисляется по формуле 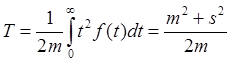, и равно m/2 только для детерминированного интервала движения.

Кстати среднее число автобусов, которые едут в противоположном направлении равно 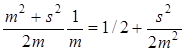, что больше ½ для случайного интервала движения.

ТМО

Практическое занятие №7 (второй семестр)

Тема: «Построение доверительных интервалов. Проверка параметрических гипотез»

План:

§ Повторение лекционного материала (свойства основных числовых характеристик);

§ Проверка отсутствующих;

§ Решение задач;

§ Контрольная работа №3;

§ Выдача домашнего задания.

Задача №1.  Время выполнения некоторого технологического процесса является случайной величиной x, имеющей нормальный закон распределения. По результатам 10-ти испытаний точечная оценка M[x] составила 14 минут, а точечная оценка s[x] равна 2,5 минуты. Для доверительной вероятности 0,9 построить доверительные интервалы для M[x] и s[x] случайной величины x. Для уровня значимости 0,1 проверить гипотезу о том, что M[x] меньше 15,5 минут.

Задача №2.  При поверке вольтметра были проведены 15 измерений. Предполагая, что ошибка измерения прибора имеет нормальный закон распределения, проверить гипотезу об отсутствии систематической ошибки измерения, если по результатам испытаний среднее арифметическое значение отклонения результатов измерения от истинного значения составило 0,05 В; а оценка дисперсии ошибки измерения составила 0,0004 В².

Задача №3.  С целью уменьшения времени выполнения некоторого технологического процесса (ТП) была проведена его модернизация. Предполагая, что время выполнения ТП имеет нормальный закон распределения, необходимо проверить гипотезу о том, что модернизация ТП не уменьшила его среднее время выполнения, если по выборке объема n=30 точечная оценка математического ожидания и среднеквадратического отклонения времени выполнения ТП после модернизации составили 5,7 часа и 0,1 часа соответственно. Среднее время выполнения ТП до модернизации составляло 6 часов. Предполагается, что модернизация не могла увеличить среднее время выполнения ТП. Вероятность совершения ошибки первого рода принять равной 0,05.

Задача №4.  Для доверительной вероятности 0,95 построить доверительный интервал для математического ожидания случайной величины, имеющей нормальное распределение, если среднеквадратическое отклонение случайной величины известно и равно 1,5 ед., а точечная оценка математического ожидания по выборке объема n=15 составила 30 ед.

Задача №5.  С целью уменьшения времени выполнения некоторого технологического процесса (ТП) была проведена его модернизация. Предполагая, что время выполнения ТП имеет нормальный закон распределения с известным среднеквадратическим отклонением, равным 0,1 часа, проверить гипотезу о том, что модернизация ТП не уменьшила его среднее время выполнения (среднее время выполнения ТП до модернизации составляло 9 часов). По выборке объема n=30 точечная оценка математического ожидания времени выполнения ТП после модернизации составили 8,7 часа. Предполагается, что модернизация никак не могла увеличить среднее время выполнения ТП. Уровень значимости принять равным 0,05.