Исследование свойств адаптивных систем с эталонными моделями: Методические указания к лабораторным работам по курсу “Адаптивные системы управления”

Министерство образования и науки  Российской Федерации

Федеральное агентство по образованию

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

 Исследование Свойств Адаптивных систем

с эталонными моделями

Методические указания к лабораторным работам по курсу “Адаптивные системы управления” для студентов специальности 220201 - "Управление и информатика в технических системах"

Новосибирск – 2006

Оглавление

1.  Лабораторная работа №1. Одноканальная система с градиентным

      алгоритмом адаптации ..................................................................................................................... 3

2.  Лабораторная работа №2. Система с пропорционально-                            интегральным алгоритмом изменения  коэффициентов регулятора, синтезированным методом скоростного градиента.................................................................................................................. 10

3.  Лабораторная работа №3. Система с алгоритмом адаптации на основе      второго метода Ляпунова.................................................................................................................. 16

4.  Лабораторная работа №4. Исследование адаптивной системы             пониженного порядка.................................................................................................................. 22

     Список рекомендуемой литературы................................................................................................................... 27

Лабораторная работа №1

 Одноканальная система с градиентным алгоритмом адаптации

Цель работы: изучение свойств системы с алгоритмом адаптации, синтезированным по градиентному методу, анализ влияния темпа параметрических возмущений на качество процессов и величину управляющего воздействия.

1.  Основные сведения

Градиентный алгоритм относится к базовым алгоритмам адаптации. Вектор градиента всегда направлен в сторону максимального локального роста функции. Следовательно, если вектор скорости настраиваемых параметров () направить в сторону антиградиента 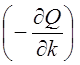, то реализуется последовательный спуск в локальный минимум

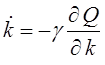                                                      (1.1)

Проведем синтез адаптивной системы для одноканального линейного объекта управления

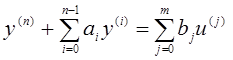                                           (1.2)

где u, y – управляющая и выходная переменные соответственно. Параметры объекта a_i, b_j точно не определены, но заданы (n + m + 1) – мерной областью возможных значений W_ab. Операторная запись уравнения (1.2) имеет вид

                                                   (1.3)

где        a_n (p) = pⁿ + a_n-1 p^n-1 + …+ a₀ ,            b_m (p) = b_m p^m + b_m-1 p^m-1 + … + b₀ ,    pⁱ = dⁱ / dtⁱ – оператор i- кратного дифференцирования.

          Цель управления зададим предельным соотношением

                                                 (1.4)

где y_м (t) – эталонная траектория движения, которая удовлетворяет уравнению эталонной модели

                                                                                (1.5)

здесь 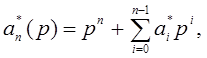  r – эталонное входное воздействие на систему. Оператор  является устойчивым, т.е. корни уравнения  имеют отрицательную действительную часть.

Для определения структуры «идеального» закона управления выполним преобразования уравнений (1.2) и (1.5). Вычтем из обеих частей уравнения (1.3) выражение (a_n (p) y):

0 = b_m (p) u – a_n (p) y .                                             (1.6)

 Полагая y = y_м , запишем уравнение (1.5)

  .                                                   (1.7)

Прибавим к обеим частям уравнения (6) выражение () :

                                  (1.8)

где 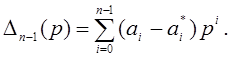 Далее вычтем из (1.8) уравнение (1.5):

                                    (1.9)

где e = y – y_м. Пусть “идеальный” закон управления имеет вид

                                         (1.10)

тогда

                                                    (1.11)

 Так как полином является устойчивым по условию, то e® 0 при t ® ¥, т.е. закон управления (1.10) позволяет обеспечить выполнение цели управления (1.4). Учитывая неизвестность коэффициентов полиномов b_m (p) и D_n-1 (p), реальный закон управления запишем в виде

                                            (1.12)

с операторами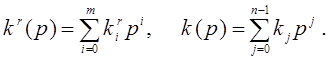

Если в процессе настройки коэффициентов регулятора (1.12) будет выполнено  при t®¥ ,  то e® 0,  что показывает достижение поставленной цели управления.

          Для определения целевой функции введем новое рассогласование (s) , которое возникает в результате замены y_м на  yв уравнении эталонной модели (1.5),

                                                 (1.13)

Если вычесть из (1.13) уравнение (1.5), то получим уравнение, описывающее связь между рассогласованиями e и s :

.                                                    (1.14)

Из (1.14) следует, что если s® 0 при t®¥, то в силу устойчивости  имеем       e® 0 при t®¥ . Следовательно, будет выполнена поставленная цель. Это позволяет задать целевую функцию в виде

                                                     (1.15)

Выполним преобразования уравнения (1.13). Просуммируем уравнения объекта (1.8) и регулятора (1.12):

,

приведем подобные и учтем (1.13):

                     (1.16)

Введем обозначения для вектора неизвестных параметров

вектора настраиваемых параметров

и вектора координатных переменных