Исследование свойств адаптивных систем с эталонными моделями: Методические указания к лабораторным работам по курсу “Адаптивные системы управления”, страница 8

          Метод вектора скорости или, в частном случае, метод старшей производной, может быть использован для синтеза алгоритма настройки коэффициентов регулятора. В процессе работы системы собирается и анализируется априори неизвестная информация о свойствах объекта управления. Основным источником такой информации являются производные выходной переменной или вектор первых производных координат состояния, отсюда название метода. Полученная информация используется в адапторе для изменения значений коэффициентов регулятора. Это позволяет создать «быстрый» адаптор для парирования быстроменяющихся возмущения.  Оценивание требуемых производных осуществляется с помощью малоинерционного линейного фильтра. Уравнение основного контура, как и в предыдущих системах, определяется  методом эталонного уравнения.

В адаптивных системах изменение параметров регулятора направлено на подавление возмущений, действующих на объект управления. Поэтому, как правило, число настраиваемых параметров определяется действующими возмущениями. Уменьшение количества контуров адаптации может являться следствием уменьшения параметрических возмущений, которые учитываются в модели объекта при неизменных условиях его функционирования. Один из способов изменения модели объекта основан на применении ряда Тейлора. Для неизвестных параметров   и аддитивного возмущения  остаются в силе предположения об ограниченности амплитуды и темпа их изменения. Данным условиям удовлетворяет большой класс объектов, например, динамические системы с периодическими коэффициентами, к которым относятся электрические контуры с переменными значениями сопротивлений. Периодическими аддитивными возмущениями могут быть моменты сопротивлений в механической системе с упругими колебаниями или в трехфазном асинхронном двигателе при переменной нагрузке, которая встречается, например, в ленточном конвейере.

2.  Методические указания

В  работе рассматривается нестационарный  линейный объект управления

          ,                                  (4.1)

где  - вектор координат состояния, y - выходная переменная,  u - управляющее воздействие, y, u , А, В, С - матрицы коэффициентов соответствующих размерностей:

,

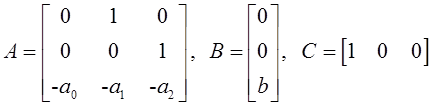где  - неизвестные коэффициенты. Желаемые свойства системы стабилизации задаются управлением эталонной модели (блок желаемой динамики)

,                                  (4.2)

здесь r – эталонный входной сигнал системы,

.

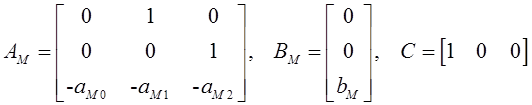Параметры модели объекта и желаемые показатели качества процессов замкнутой системы приведены в таблице 2; статическая ошибка допускается равной 5%.  Закон управления определяется методом эталонного уравнения,

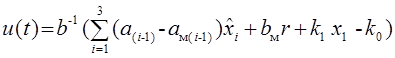 ,                             (4.3)

где - оценки координат состояния.  Изменение  осуществляется согласно алгоритмам адаптации

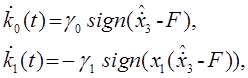
или 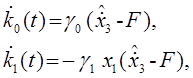                                                                                            (4.4)

где  , F – функция, описывающая желаемые динамические свойства замкнутой системы. Оценки координат состояния   получаются с помощью линейного фильтра

                                                 (4.5)

где μ- малый параметр,  A_ф, В_ф, С_ф – матрицы коэффициентов, причем A_ф – гурвицева матрица,

.

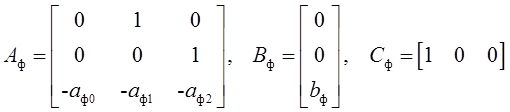С учетом уравнений фильтра (4.5) и эталонной модели (4.2) функция F(·) определяется следующим образом

,

Структурная схема адаптивной системы с вектором скорости пониженного порядка изображена на рисунок 4.1.

          Адаптивная система (4.1), (4.3)- (4.5)  имеет пониженный порядок, так как  парирование трех параметрических возмущений  и одного аддитивного возмущения  осуществляется с помощью двух контуров адаптации.

3.  Порядок выполнения  работы

3.1 Определить  элементы матриц ,, по заданным показателям к качеству процессов (см. таблицу 2).

3.2  Определить элементы матриц ,, выбирая .

3.3 Собрать схему адаптивной системы (рисунок 4.1).

3.4  Получить графики переходной характеристики системы (y(t)), управляющего воздействия (u(t)) и процессов на выходе адаптора () при r(t)=1(t), M(t)=0, нулевых начальных условиях, ==1. Определить показатели качества (s%, ,  - время сходимости процессов в адапторе).

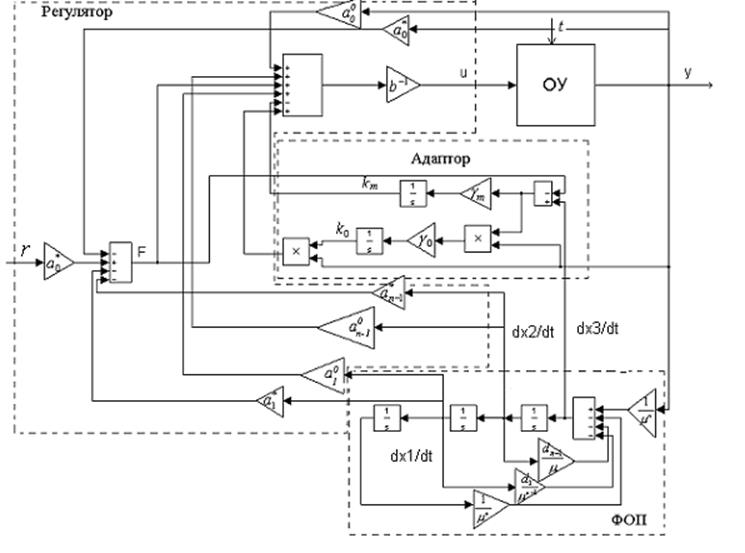
Рисунок 4.1

3.5  Выполнить п.3.4 при .