Исследование свойств адаптивных систем с эталонными моделями: Методические указания к лабораторным работам по курсу “Адаптивные системы управления”, страница 5

          Структурная схема замкнутой системы приведена на рисунке 2.2. Система состоит из  четырех основных блоков: объект управления (ОУ), модель (М), адаптивный регулятор (АР), адаптор (А). Для формирования коэффициентов регулятора и управляющего воздействия используется первая производная выходной переменной Как правило, производная выходного сигнала не может быть измерена, поэтому требуется включение в систему либо наблюдателя, либо фильтра оценки производных. Порядок фильтра может быть равен или быть на единицу меньше порядка объекта. Постоянная времени фильтра выбирается на один или два порядка меньше, чем минимальная постоянная времени эталонной модели. Структурная схема системы с нестационарным объектом и фильтром оценки производных второго порядка изображена на рисунке 2.3. Моделирование адаптивной системы рекомендуется выполнять в среде MatLab, приложение Simulink.

3. Порядок работы

3.1 Определить  элементы матриц ,,по заданным требованиям к качеству процессов, статическая ошибка работы системы допускается равной 5% (см. Таблицу1).

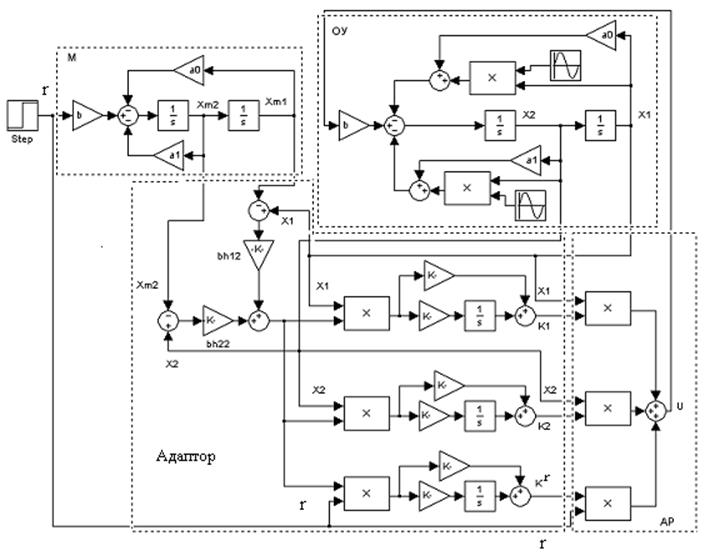
Рисунок 2.2

3.2 Вычислить элементы матриц H как решение уравнения Ляпунова (2.19) при

.

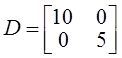Записать уравнения алгоритмов адаптации (2.20)-(2.22) с вычисленными значениями коэффициентов.

3.3 Собрать схему адаптивной системы (рисунок 2.2), объект управления моделировать по схеме, приведенной на рисунке 1.1.

3.4 Получить графики переходной характеристики системы (y(t)), управляющего воздействия (u(t)) и процессов на выходе адаптера () при r(t)=1(t), нулевых начальных условиях на интегрирующих элементах, g =g₁=1. Определить показатели качества (s%, ,  -время сходимости процессов в адаптере).

3.5 Изменить значения коэффициентов (=1, =10 и =10, ₁= 10) сравнить переходные характеристики и процессы в адаптере с результатами п.3.4 по показателям качества.

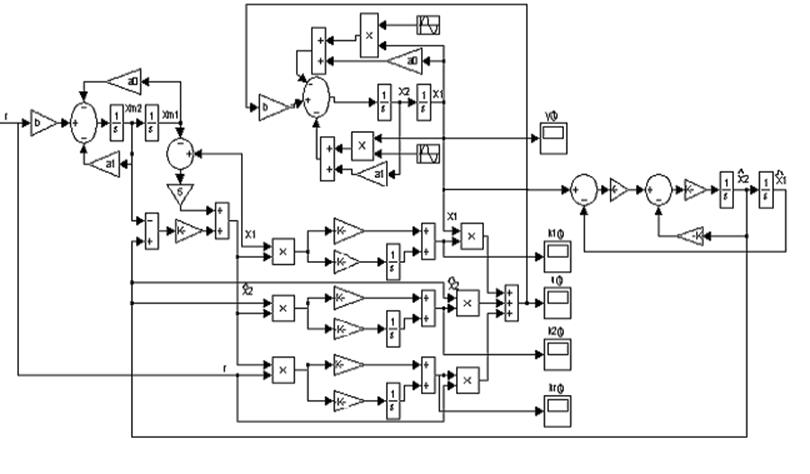Рисунок 2.3

3.6 Изменить начальные условия в объекте (,), получить вид y(t), u(t), , ,. Моделирование провести при  g==1, =1, =10.Сравнить с результатами   п.3.4.

3.7 Изменить последовательно параметры объекта  в 2 раза,  выполнить п.3.4,  с

помощью коэффициентов передачи адаптора добиться желаемого качества процессов.

3.8 Изменить модель объекта управления:  ,  (рисунок 1.2). Провести моделирование при нулевых начальных условиях и различных значениях :   а) =1, =1,   б) =1, =10,    в) =10, =1. Для улучшения процессов в системе изменить значения , . Сравнить с результатами  п.3.4.

3.9^* Построить зависимость u_maxот  a, u_max = max |u(t)| (при ), , 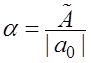где t_k - время наблюдения за процессами в системе. Амплитуду параметрических возмущений выбирать из диапазона (0.1÷100), например, (0.1, 1, 10, 50, 100), . Если с увеличением  система становится неустойчивой, то следует подбором значений γ вернуть систему в устойчивое состояние.

 3.10 Рассчитать параметры фильтра оценки производных второго порядка. Собрать схему системы с фильтром (рисунок 2.3). Повторить пп.3.5, 3.8.

4. Содержание отчета

4.1 Цель работы.

4.2 Исходные данные.

4.3 Структурная схема адаптивной системы.

4.4 Расчет параметров (пп.3.1, 3.2, 3.11). Уравнения адаптивной системы и фильтра с вычисленными значениями параметров.

4.5 Графики процессов пп. 3.3, 3.5 – 3.11, график зависимости  u_maxот  a.

4.6 Выводы по работе.

5. Контрольные вопросы

5.1 Виды и источники неопределённостей.

5.2 Виды возмущений.

5.3 Целевые критерии.

5.4 Агоритм скоростного градиента, формы алгоритма.

5.5 Вывод пропорционально-интегрального алгоритма адаптации для системы с объектом второго порядка и целевым функционалом (2.6).

5.6 Влияние начальных условий в адапторе на свойства системы.

5.7 Влияние начальных условий в объекте на свойства системы.

5.8 Влияние темпа параметрических возмущений на свойства системы.

5.9 Структурная схема адаптивной системы, функции основных блоков системы.

5.10 Расчет параметров фильтра оценки производных.

Лабораторная работа №3

Система с алгоритмом адаптации на основе второго метода Ляпунова

Цель работы: изучение свойств непрерывной адаптивной системы, синтезированной на основе второго метода Ляпунова; исследование влияния параметров возмущений на качество работы системы.

1.  Основные сведения