где e (t) = x (t) – xм (t). Предлагаем выполнение условия управляемости объекта и наблюдаемости координат состояния.
Пусть целевой функционал выбран в форме скалярной квадратичной функции
![]() (2.6)
(2.6)
Поставленная цель управления выполняется, если Q®0 при t®¥.
Уравнение основного контура можно получить модальным методом, т.е. разрешив уравнение
![]()
относительно u (t):
![]()
или
![]() (2.7)
(2.7)
«Идеальное» управление можно записать в форме
![]() (2.8)
(2.8)
где матрицы k*x, k*r удовлетворяют условию
![]()
![]()
![]() . (2.9)
. (2.9)
Матрицы идеальных значений коэффициентов регулятора k*x, k*r существуют, если выполняются ранговые условия
![]()
Реальный закон управления имеет вид
![]() (2.10)
(2.10)
где
kx (t), kr (t) – матрицы настраиваемых коэффициентов регулятора, ![]()
Для определения вида алгоритма адаптации требуется вычислить производную целевого функционала (2.6) в силу уравнений системы (2.3), (2.4), (2.10):
![]() (2.11)
(2.11)
После подстановки (2.10) в (2.11) имеем
![]()
![]() . (2.12)
. (2.12)
Определим скоростные градиенты
![]() ,
,
![]() .
.
Для алгоритмов настройки коэффициентов выбираем АСГ в дифференциальной форме (2.2)
![]() (2.13)
(2.13)
где Г = gI, g > 0 .
Система (2.3), (2.4), (2.10), (2.13) относится к системам с параметрической адаптацией. На основе АСГ можно синтезировать системы с сигнальной и сигнально- параметрической адаптацией. Системы с алгоритмом адаптации (2.13) сохраняют работоспособность при изменении координатных и параметрических возмущений в широких пределах. Качество процессов ухудшается, если скорость изменения параметрических возмущений высокая.
С целью повышения быстродействия в контурах параметрической настройки коэффициентов регулятора можно применять пропорционально-интегральные алгоритмы адаптации в дифференциальной форме
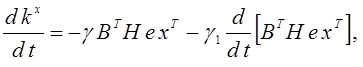
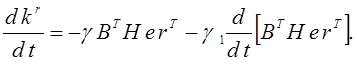 (2.14)
(2.14)
2. Методические указания
Рассматривается линейный одноканальный объект управления (1.18), (1.19) с параметрическими возмущениями. Желаемая динамика системы задана уравнением эталонной модели (1.20) по требованиям к качеству переходных процессов (таблица1). В системе эталонная модель реализуется в виде линейного динамического звена. Согласно методу эталонного уравнения получим описание регулятора:
![]() (2.15)
(2.15)
или ![]() ,
(2.16)
,
(2.16)
где
![]() =
=![]() ,
, ![]() ,
, ![]() -настраиваемые
коэффициенты регулятора, изменение которых осуществляется по
пропорционально-интегральному алгоритму (2.14):
-настраиваемые
коэффициенты регулятора, изменение которых осуществляется по
пропорционально-интегральному алгоритму (2.14):
![]() =
=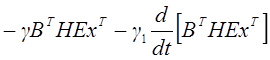 ,
(2.17)
,
(2.17)
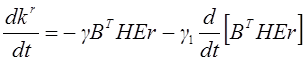 , (2.18)
, (2.18)
где
![]() ,
, ![]() -
матрица коэффициентов, удовлетворяющая уравнению Ляпунова
-
матрица коэффициентов, удовлетворяющая уравнению Ляпунова
![]() = - D
. (2.19)
= - D
. (2.19)
Уравнения (2.17), (2.18) можно записать в виде
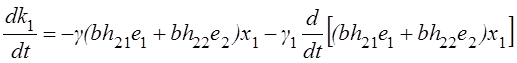 ,
(2.20)
,
(2.20)
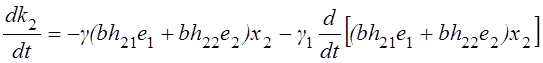 ,
(2.21)
,
(2.21)
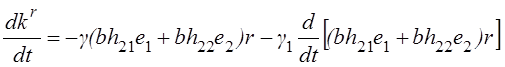 .
(2.22)
.
(2.22)
Дифференциальные уравнения (2.17), (2.18) или (2.20)-(2.22) описывают адаптор, структурная схема которого изображена на рисунок 2.1.
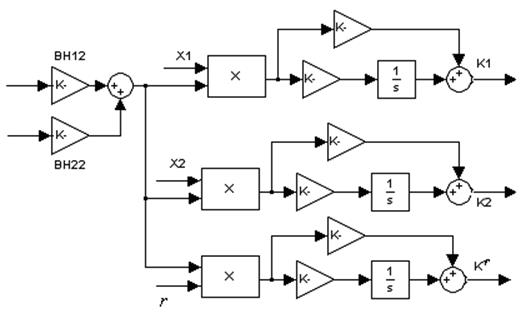
Рисунок 2.1
Быстродействие адаптора определяется с
помощью времени сходимости процессов (![]() ),
которое определяется аналогично
),
которое определяется аналогично ![]() , но по графикам
, но по графикам ![]() , i – индекс настраиваемого коэффициента регулятора. В случае
пятипроцентных отклонений область установившихся значений коэффициентов
задается неравенством
, i – индекс настраиваемого коэффициента регулятора. В случае
пятипроцентных отклонений область установившихся значений коэффициентов
задается неравенством
![]() ,
,
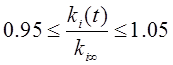 ,
, ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.