Уравнение для рассогласования (16) примет вид
![]() .
(1.17)
.
(1.17)
Алгоритм настройки коэффициентов согласно (1.1), (1.15), (1.17) имеет вид
![]()
или ![]() .
.
2. Методические указания
Объект управления имеет математическую модель вида:
![]() = A x + B u, y = C x,
(1.18)
= A x + B u, y = C x,
(1.18)
где ![]() - вектор координат
состояния, y
- выходная переменная, u - управляющее воздействие, y, u Î
- вектор координат
состояния, y
- выходная переменная, u - управляющее воздействие, y, u Î ![]() ; A, B, C - матрицы коэффициентов
соответствующих размерностей;
; A, B, C - матрицы коэффициентов
соответствующих размерностей;
A=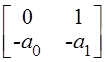 , B=
, B=![]() , C=
, C=![]() , (1.19)
, (1.19)
здесь ![]() ,
, ![]() , b-
неизвестные коэффициенты, которые могут быть как постоянными, так и
переменными. Стационарный объект управления моделируется по схеме, изображенной
на рисунке 1.1, нестационарный – по схеме, представленной на рисунке 1.2.
Желаемое поведение системы описывают уравнения эталонной модели:
, b-
неизвестные коэффициенты, которые могут быть как постоянными, так и
переменными. Стационарный объект управления моделируется по схеме, изображенной
на рисунке 1.1, нестационарный – по схеме, представленной на рисунке 1.2.
Желаемое поведение системы описывают уравнения эталонной модели:
![]()
![]() , (1.20)
, (1.20)
где r - входная переменная,
![]() =
=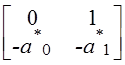 ,
, ![]() =
=![]() ,
, ![]() =
=![]() .
.
Коэффициенты а0*, а1*, b* определяются по заданным показателям качества переходного процесса, приведенным в табл.1, статическая ошибка работы системы допускается равной 5%.
Закон управления формируется в виде:
![]()
или
![]() . (1.21)
. (1.21)
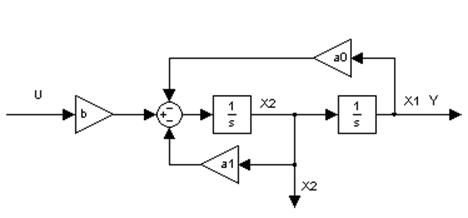
Рисунок 1.1
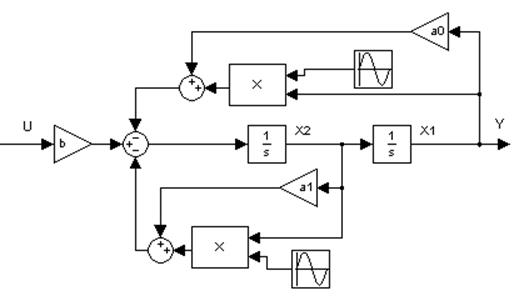
Рисунок 1.2
Коэффициенты регулятора изменяются по градиентному алгоритму адаптации:
![]() ,
,
![]() ,
(1.22)
,
(1.22)
![]() ,
,
![]() .
.
Структурная схема системы с градиентным алгоритмом адаптации (1.18) – (1.22) изображена на рисунке 1.3. В данном случае предполагается «идеальное» измерение требуемых производных выходных переменных. Однако в большинстве реальных технических систем для оценки производных требуется введение наблюдателя состояния или фильтра оценки производных.
Уравнение асимптотического наблюдателя (идентификатора) имеет вид
![]() ,
,
где
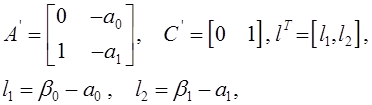
причем ![]() - желаемый
характеристический многочлен наблюдателя, коэффициенты которого определяются,
исходя из требований к динамическим свойствам:
- желаемый
характеристический многочлен наблюдателя, коэффициенты которого определяются,
исходя из требований к динамическим свойствам: ![]() .
Заметим, что
.
Заметим, что
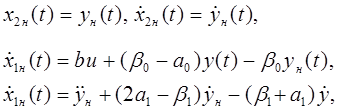
причем
![]() ,
, ![]() . Для старшей производной выходной переменной
наблюдателя, которая является оценкой соответствующей производной выходной
переменной системы, справедливо выражение
. Для старшей производной выходной переменной
наблюдателя, которая является оценкой соответствующей производной выходной
переменной системы, справедливо выражение
![]() или
или ![]() .
.
Структурная схема адаптивной системы с наблюдателем изображена на рисунке 1.4.
Качество
работы адаптивной системы оценить с помощью показателей: перерегулирование (s%),
установившаяся ошибка (![]() ),
),
s % =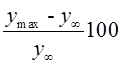 ,
, ![]() ,
, ![]() =
=![]() ,
,
где ![]() - максимальное значение
выходной переменной. Оценкой быстродействия системы выбрано время переходного
процесса (
- максимальное значение
выходной переменной. Оценкой быстродействия системы выбрано время переходного
процесса (![]() ), которое равно интервалу времени с начала
работы системы до момента установления значения выходной переменной в диапазоне
), которое равно интервалу времени с начала
работы системы до момента установления значения выходной переменной в диапазоне
![]() .
.
Моделирование адаптивной системы рекомендуется выполнять в среде MatLab, приложение Simulink.
3. Порядок выполнения работы
3.1
Определить элементы матриц ![]() ,
,![]() ,
,![]() по заданным требованиям к качеству
процессов (см. таблицу 1).
по заданным требованиям к качеству
процессов (см. таблицу 1).
3.2
Выполнить моделирование стационарного (рисунок1.1) и нестационарного (рисунок
1.2, ![]() =10,
=10, ![]() =1)
объектов, оценить устойчивость, определить показатели качества ( σ %, tn ).
=1)
объектов, оценить устойчивость, определить показатели качества ( σ %, tn ).
3.3
Собрать схему эталонной модели на интегрирующих элементах. Получить переходную
характеристику (r=1(t), ![]() ). Определить показатели качества ( σ %, tn ).
). Определить показатели качества ( σ %, tn ).
3.4 Собрать схему адаптивной системы (1.18), (1.20)-(1.22). Параметры объекта управления приведены в таблице 1, схема моделирования объекта - рисунок 1.1. Структурная схема адаптивной системы изображена на рисунке 1.3.
3.5
Получить графики переходной характеристики системы (y(t)),
управляющего воздействия и процессов на
выходе адаптора (![]() ) при r(t)=1(t), нулевых начальных условиях, кроме
) при r(t)=1(t), нулевых начальных условиях, кроме ![]() , γ=10 в контурах
настройки
, γ=10 в контурах
настройки ![]() и γ r = 0.001 в
контуре настройки
и γ r = 0.001 в
контуре настройки ![]() .
.
3.6 Определить показатели качества, сравнить их значения с заданными. Если качество процесса неудовлетворительное, то изменяя γ, добиться достижения требуемых показателей.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.