Исследование свойств адаптивных систем с эталонными моделями: Методические указания к лабораторным работам по курсу “Адаптивные системы управления”, страница 3

3.7 Изменить начальные условия в объекте (), получить вид y(t), (t), (t), (t), u (t). Моделирование провести для различных значений g. Сравнить с результатами п.3.5. Изобразить зависимость γ от x₁(0) при γ ^r = 0.001 иx₂(0)= 0.

3.8 Изменить модель объекта управления (рисунок 1.2), , . Провести моделирование адаптивной системы при нулевых начальных  условиях, кроме (0), (0) = 1, и различных значениях , : а) =1, =1,   б) =1, =10,  в) =10, =1.  Для улучшения процессов в системе изменить значения γ в 10 раз. Сравнить с результатами п.3.5.

3.9  Рассчитать параметры наблюдателя. Собрать схему системы с наблюдателем

(рисунок 1.4). Повторить пп. 3.4, 3.8.

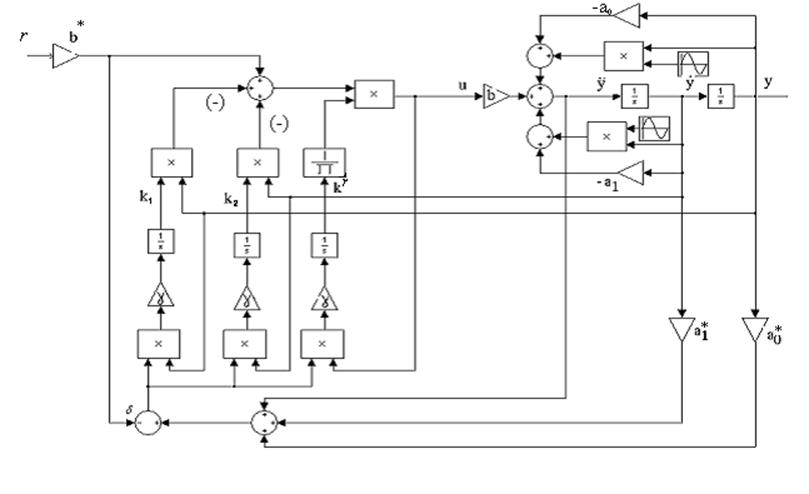
Рисунок 1.3

Таблица 1

N			b	s%
1	2	3	2	0	2
2	1	4	1	10	4
3	4	2	4	20	5
4	4	1	4	0	4
5	0,1	0,5	0,1	30	10
6	2	10	2	0	2
7	10	2	10	0	5
8	0.5	1.5	0.5	5	3

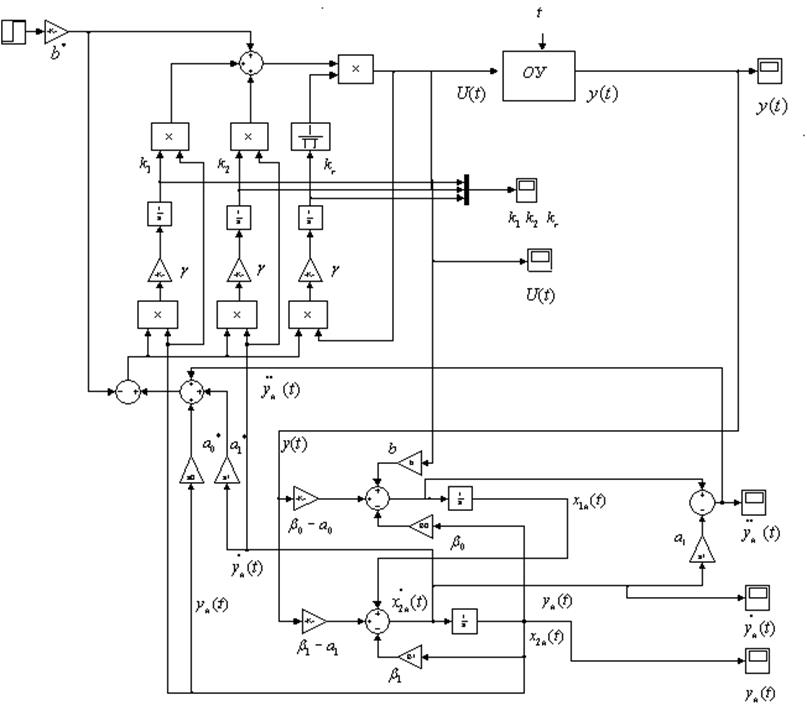
Рисунок 1.4

4.  Содержание отчета

4.1 Цель работы.

4.2 Исходные данные.

4.4 Структурная схема адаптивной системы.

4.5 Расчет параметров адаптивного регулятора и наблюдателя.

4.6 Уравнения адаптивной системы с наблюдателем и вычисленными значениями параметров.

4.7 Графики процессов пп. 3.2 – 3.10, график зависимости u_maxот  a.

4.8 Выводы по работе.

5. Контрольные вопросы

5.1 Классификация адаптивных систем.

5.2 Виды эталонных моделей, способы реализации.

5.3 Блок-схемы беспоисковых систем с моделью.

5.4 Основные блоки системы с градиентным алгоритмом адаптации.

5.5 Влияние начальных условий в адапторе на свойства системы.

5.6 Уравнение адаптивного закона управления.

5.7 Влияние темпа параметрических возмущений на свойства системы.

5.8 Расчет асимптотического наблюдателя.

5.9 Определение вида алгоритма адаптации, использованного в лабораторной работе.

Лабораторная работа №2

система с пропорционально-интегральным алгоритмом изменения  коэффициентов регулятора, синтезированным методом скоростного градиента

Цель работы: исследование свойств системы стабилизации, в которой коэффициенты регулятора изменяются по алгоритму скоростного градиента в конечно-дифференциальной форме.

1.  Основные сведения

Суть метода скоростного градиента заключается в следующем:  настройка параметров осуществляется в направлении, противоположном скорости изменения целевого функционала вдоль траектории обобщенного настраиваемого объекта (ОНО). Алгоритмом скоростного градиента называется правило изменения вектора настраиваемых коэффициентов (q), задаваемое  уравнением вида

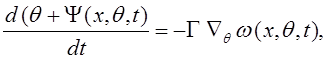                                          (2.1)

где Ñ- дифференциальный оператор, Г = Г ^Т > 0 – квадратная матрица коэффициентов передачи,

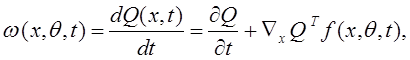
здесь Q(.) – целевой функционал, f (x,q,t) – вектор- функция, описывающая ОНО,

y (.) – некоторая вектор-функция, удовлетворяющая условию псевдоградиентности

АСГ вида (2.1) называют алгоритмом в конечно-дифференциальной форме. Частным случаем (2.1) являются алгоритмы в дифференциальной форме (в случае y = 0)

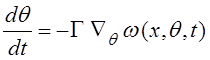                                      (2.2)

и в конечной форме (для Г = 0)

,

где g - шаг дискретизации.

Рассмотрим пример синтеза системы  с параметрической адаптацией. Объект управления задан моделью в пространстве состояний

                                       (2.3)

где xÎRⁿ , uÎR^m – векторы состояния и входа  ОУ,  А, B – неизвестные матрицы коэффициентов.

Эталонная модель выбрана в форме

                                     (2.4)

где rÎR^m– задающее воздействие, А_м – гурвицева матрица.

Цель управления сформирована относительно координатного рассогласования

                                              (2.5)