В данном случае основной контур (3.1) описывается уравнением
,
(3.4)
где k0 = const. Алгоритм адаптации (3.2), (3.3) преобразуется к виду:
,
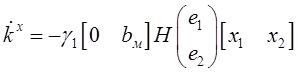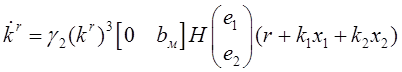, (3.5)
где
γ1, γ2 = const - коэффициенты передачи адаптора, e1= x1- xM1, e2= x2- xM2, xM1 =yM, xM2=
, kx = 
, dimH =2 x 2, H = const, H
= HT, H > 0, H- матрица
коэффициентов квадратичной формы, выбранной для исследования устойчивости
адаптивной системы, V = xT Hx. Элементы
матрицы H определяются как решение матричного уравнения
Ляпунова
= - Q
, Q = QT, Q > 0 . (3.6)
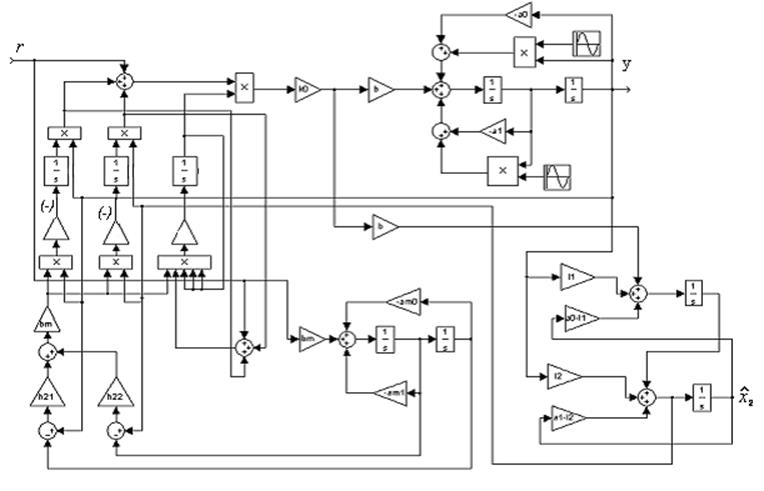
Схема системы с нестационарным объектом управления и измеряемой производной выходной переменной изображена на рисунке 3.1.
3. Порядок работы
3.1
Определить элементы матриц 
, 
, 
по
заданным требованиям к качеству процессов (см. таблицу 1).
3.2 Вычислить элементы матриц H как решение уравнения Ляпунова (3.6), полагая
.
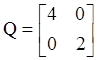3.3 Записать уравнения алгоритмов адаптации (3.5) с вычисленными значениями коэффициентов.
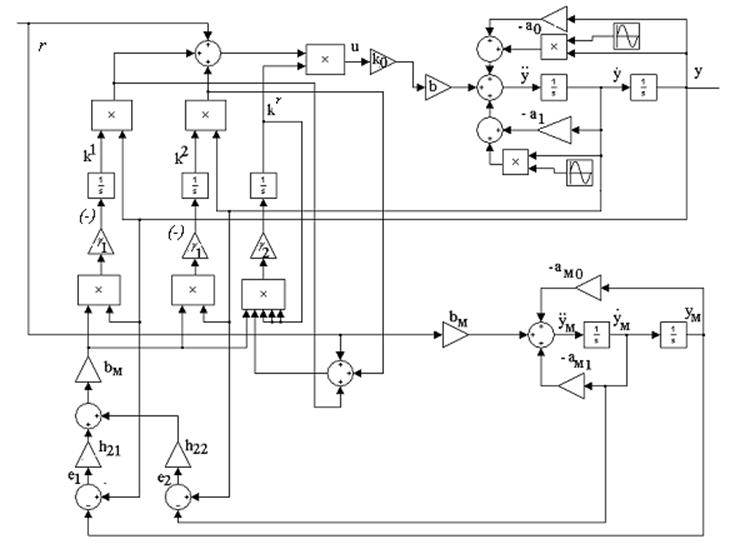
Рисунок 3.1
3.4
Собрать схему эталонной модели (1.20) на интегрирующих элементах. Получить
переходную характеристику 
. Определить показатели
качества: σ%, tn.
3.5
Собрать схему адаптивной системы (рисунок 3.1), объект управления моделировать
по схеме, приведенной на рисунке 1.1 (см. лаб. работу № 1). Получить графики
переходной характеристики системы (y(t)), управляющего воздействия (u(t))
и процессов на выходе адаптера (
) при r(t)=1(t), нулевых начальных условиях по координатам состояния, 
=10, 
=1, kr(0)=1.
Определить показатели качества (s%, 
,
).
|
|
|
3.6
Изменить значения коэффициентов передачи адаптора так, чтобы показатели
качества выходного процесса соответствовали эталонным значениям, полученным в
п.3.4. Сравнить переходные характеристики и процессы в адаптере с результатами
п.3.5 по s%, 
, .
3.7
Изменить начальные условия в объекте (
(0)=1), получить вид
y(t), u(t), 
(t), 
(t),
(t).
Моделирование провести при g2=1 и
различных g1 : g1=1,
g1=10. Сравнить результат с п. 3.5.
3.8
Изменить последовательно параметры объекта 
,
, b в 2 раза, выполнить задание п.
3.5.
3.9
Изменить модель объекта управления 
, 
. Провести моделирование при нулевых начальных
условиях и различных значениях 
, 
: а) =1, =1, б) =1, =10, в) =10, =1. Для достижения эталонных показателей
качества изменить значения 
, 
.
3.10* Построить зависимость umaxот a (см. п.3.8 лаб. работы №1).
3.11 Выполнить расчет наблюдателя состояния (см. методические указания к лаб. работе №1). Собрать схему системы с наблюдателем (рисунок 3.2). Выполнить исследование системы, повторив пп. 3.5, 3.6, 3.9.
4. Содержание отчета
4.1 Цель работы.
4.2 Исходные данные.
4.4 Структурная схема адаптивной системы.
4.5 Расчет параметров адаптивного регулятора и наблюдателя; уравнения адаптивной системы с вычисленными значениями параметров.
4.6 Графики процессов пп. 3.4 – 3.11, график зависимости umaxот a.
4.7 Выводы по работе.
5. Контрольные вопросы
5.1 Гипотеза квазистационарности.
5.2 Постановка задачи адаптивного управления.
5.3 Основные этапы синтеза беспоисковых адаптивных систем.
5.4 Последовательность расчета адаптивной системы на основе второго метода Ляпунова.
5.5 Влияние начальных условий в адапторе на свойства системы.
5.6 Влияние темпа параметрических возмущений на свойства системы.
5.7 Определение закона управления.
5.8 Определение алгоритма адаптации.
5.9 Структурная схема адаптивной системы.
Лабораторная работа №4
Цель работы: изучение свойств системы с алгоритмом адаптации, синтезированным по методу старшей производной, исследование возможности понижения порядка адаптивного регулятора.
1. Основные сведения
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
