С СИНХРОННЫМ ДЕТЕКТИРОВАНИЕМ
1. Цель работы
Знакомство с принципом построения и работой системы поиска экстремума, в которой оценка градиента выходной характеристики осуществляется методом синхронного детектирования.
2. Основные сведения
В работе исследуется объект управления, динамическая часть которого описывается уравнением
![]() , (1.1)
, (1.1)
а экстремальная характеристика (ЭХ) имеет вид
![]() . (1.2)
. (1.2)
Требуется организовать автоматический поиск экстремума и стабилизировать систему в этой точке.
С этой целью сформируем градиентный закон управления
![]() ,
(1.3)
,
(1.3)
где
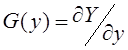 - градиент, для оценки которого используем метод
синхронного детектирования.
- градиент, для оценки которого используем метод
синхронного детектирования.
Идея
метода синхронного детектирования заключается в том, что к входному сигналу ![]() , поступающему на экстремальную
характеристику, добавляется вспомогательный поисковый синусоидальный сигнал
малой амплитуды и высокой частоты
, поступающему на экстремальную
характеристику, добавляется вспомогательный поисковый синусоидальный сигнал
малой амплитуды и высокой частоты
![]() . (1.4)
. (1.4)
Величина
и фаза колебаний, порождённых поисковым сигналом на выходе объекта, зависит от
того, какой части экстремальной характеристики соответствует значение ![]() . Если рабочая точка находится правее точки
минимума, то фаза выходных колебаний совпадает с фазой входных. Если левее – входные
и выходные колебания находятся в противофазе. Кроме того, чем дальше значение
. Если рабочая точка находится правее точки
минимума, то фаза выходных колебаний совпадает с фазой входных. Если левее – входные
и выходные колебания находятся в противофазе. Кроме того, чем дальше значение ![]() от экстремального, тем больше амплитуда
колебаний на выходе объекта.
от экстремального, тем больше амплитуда
колебаний на выходе объекта.
Сравнение
фазы входного и выходного сигналов экстремальной характеристики позволяет
определить направление движения к экстремуму (т.е. знак градиента). В качестве
фазочувствительного устройства используется блок перемножения (БП). Применение
дополнительного фильтра (Ф) позволяет получить сигнал, пропорциональный
градиенту ![]() .
.
Функциональная схема исследуемой системы приведена на рис.1.1.
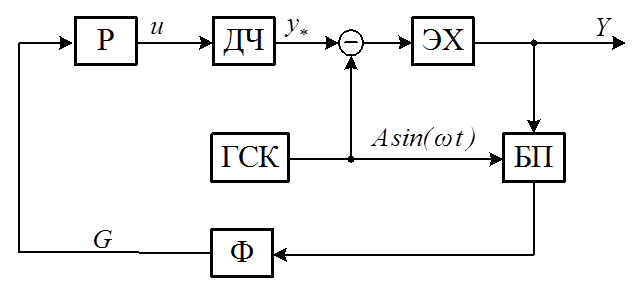
Рис.1.1. Функциональная схема системы
Р – регулятор,
ДЧ – динамическая часть объекта,
ЭХ – экстремальная характеристика,
ГСК – генератор синусоидальных колебаний,
БП – блок перемножения,
Ф – усредняющий фильтр.
3. Методические указания
3.1. При моделировании с помощью программы «Компас» в качестве генератора поисковых синусоидальных колебаний используется звено «ГАРМ».
3.2. Усредняющий фильтр представляет собой апериодическое звено с параметрами: Tф=1; kф=1.
4. Порядок выполнения работы
4.1. На основе функциональной схемы (рис.1.1) собрать схему моделирования системы, параметры которой приведены в таблице 1.1.
Задать следующие поисковых колебаний: A=0,2; щ=10.
4.2. Выбирая
различные начальные условия из диапазона ![]() =(1ч5)
и
=(1ч5)
и ![]() =-(1ч5), зарисовать переходные процессы
=-(1ч5), зарисовать переходные процессы
![]() ,
, ![]() и
портрет системы на плоскости (y, Y).
и
портрет системы на плоскости (y, Y).
Таблица 1.1
|
Вариант Параметр |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
b |
2 |
3 |
1 |
3 |
2 |
1 |
4 |
2 |
|
T |
10 |
8 |
7 |
9 |
6 |
8 |
10 |
5 |
|
a |
2 |
1 |
0,5 |
1 |
0,6 |
2 |
0,5 |
3 |
|
K |
3 |
5 |
4 |
2 |
3 |
5 |
2 |
4 |
4.3. Для одного
значения начальных условий исследовать влияние К на скорость сходимости
к экстремуму по характеристике ![]() , задавая K из
диапазона (1ч10).
, задавая K из
диапазона (1ч10).
4.4. Оценить влияние
амплитуды поисковых колебаний на характер движения к экстремуму, изменяя А
в диапазоне (0,1ч1). Зарисовать переходные процессы системы ![]() ,
, ![]() и
процесс движения к экстремуму на плоскости (y, Y).
и
процесс движения к экстремуму на плоскости (y, Y).
4.5. Задавая щ=(0,1ч10),
исследовать влияние частоты поисковых колебаний на вид процессов ![]() ,
, ![]() и процесс
движения к экстремуму на плоскости (y, Y).
и процесс
движения к экстремуму на плоскости (y, Y).
4.6. Исследовать
влияние постоянной времени фильтра на характер процессов, выбирая Tф=(1ч10). Сравнить результаты с процессами,
полученными в п.4.2. Зарисовать переходные процессы ![]() и
и ![]() .
.
5. Содержание отчёта
5.1. Цель работы.
5.2. Схема моделирования замкнутой системы.
5.3. Графики всех переходных процессов и фазовых портретов.
5.4. Выводы по работе.
6. Контрольные вопросы
6.1. Какова роль градиента в системе поиска экстремума?
6.2. С какой целью в систему вводят усредняющий фильтр?
6.3. Как влияют параметры генератора синусоидальных колебаний на оценку градиента?
6.4. Как выбрать амплитуду и частоту генератора синусоидальных колебаний?
6.5. Как в замкнутой системе можно обеспечить заданное время выхода на экстремум?
6.6. Каким образом осуществляется стабилизация системы в точке экстремума?
Лабораторная работа №2
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.