Система с настройкой коэффициентов регулятора на основе алгоритма скоростного градиента

Министерство Образования РФ

Новосибирский государственный технический университет

Кафедра Автоматики

Лабораторная работа №2

система с настройкой коэффициентов регулятора на основе алгоритма скоростного градиента

Факультет: АВТ

Группа: АА-06

Студенты:  Рампилова С.Б.                                                       Преподаватель:      Мисюркеев А.И.                                                             Шпилевая О.Я.

                    Кошкина Е.В.

Отметка о защите:

г. Новосибирск

2004 г

Цель работы: исследование свойств системы стабилизации, в которой коэффициенты регулятора изменяются по пропорционально-интегральному  алгоритму скоростного градиента в дифференциальной форме.

Исходные данные:  исходные данные представлены в таблице1.

Таблица 1.

Выполнение работы

1.  Определить  элементы матриц ,, по заданным требованиям к качеству процессов (см. Таблицу 1).

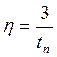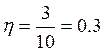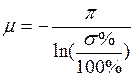,                   ,      ,      μ = 2.62,

μ = tg(φ),                   φ = 69 ⁰,            

p₁= -1 , p₂= - 7   à   a_0м = 7,  a_1м = 8,  b_м = 7.

2. Вычислить элементы матриц H как решение уравнения Ляпунова при

.

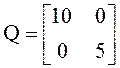Записать уравнения алгоритмов адаптации (2.20)-(2.22) с вычисленными значениями коэффициентов.

3. Собрать схему эталонной модели на интегрирующих элементах. Снять переходную характеристику . Определить показатели качества.

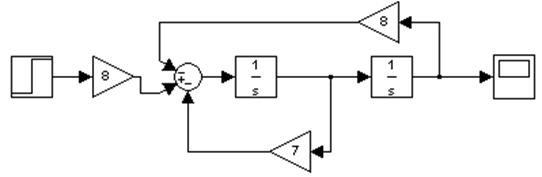
Рисунок 1. Структурная схема эталонной модели объекта

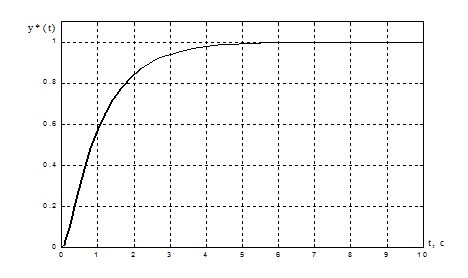
Рисунок 2. Переходная характеристика эталонной модели: s% = 0%, = 6 с.

4. Собрать схему адаптивной системы.

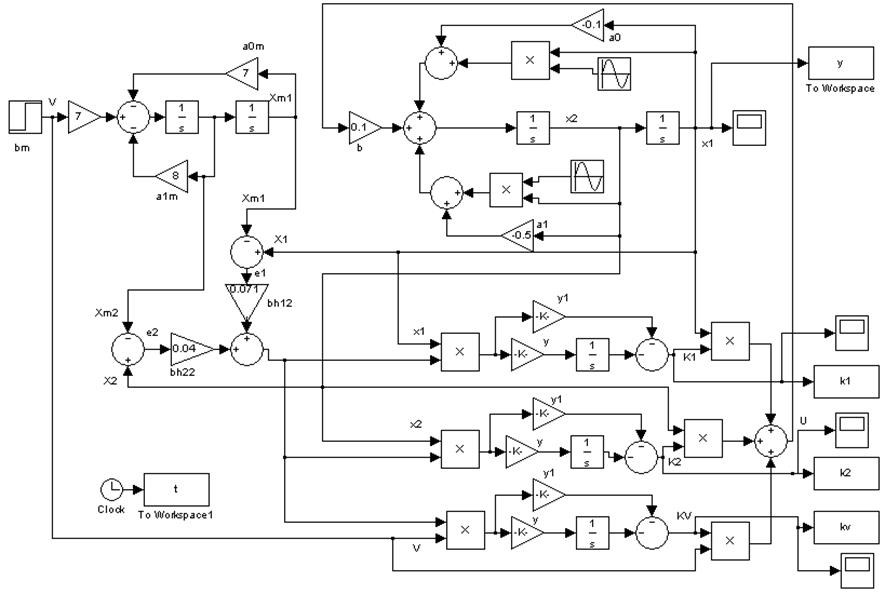
Рисунок 3. Схема адаптивной системы

5. Снять переходную характеристику системы (y(t)) и процессы на выходе адаптера () при r(t)=1(t), нулевых начальных условиях на интегрирующих элементах, g =g₁=1. Определить показатели качества (s%, ,  -время сходимости процессов в адаптере).

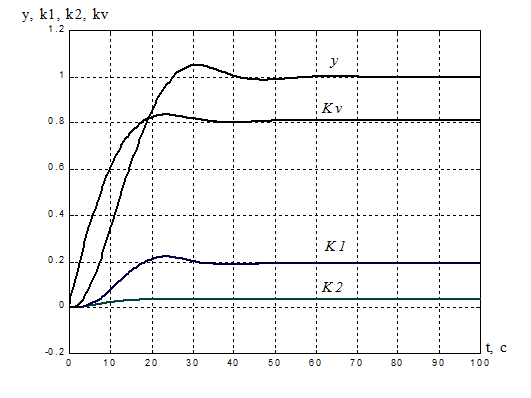
Рисунок 4. Переходная характеристика адаптивной системы y(t): s% = 5%, = 23 с.

 Процессы на выходе адаптера:

k₁(t)= 0.192,   t_паk1= 30,4 с;

 k₂(t) =0.0334,   t_паk2= 16,5 c;

k_V(t) = 0.809,   t_паkv= 15,33 с.

6. Изменить значения коэффициентов (=1, =10 и =10, ₁= 10) сравнить переходные характеристики и процессы в адаптере с результатами п.3.5 по показателям качества.

А) =1, =10

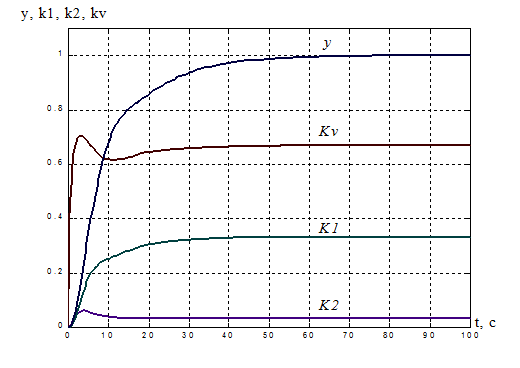
Рисунок 5. Переходная характеристика адаптивной системы y(t): s% = 0%, = 33 с.

 Процессы на выходе адаптера:

k₁(t) = 0.332,   t_паk1= 25,4 с;

 k₂(t) = 0.03207,   t_паk2= 12,6 c;

k_V(t) =0.668,  t_паkv= 17,2 с.

б) =10, ₁= 10

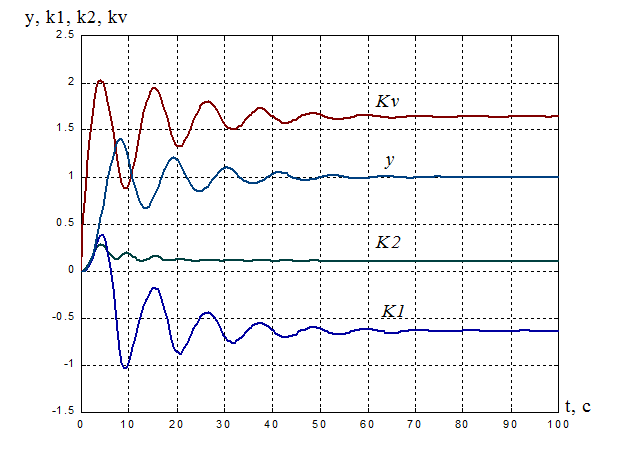
Рисунок 6. Переходная характеристика адаптивной системы y(t): s% = 40%, = 37,5 с.

 Процессы на выходе адаптера:

k₁(t) =-0.64,   t_паk1= 49,56 с;

 k₂(t) =0.1126,   t_паk2= 27,82 c;

k_V(t) =1.64,   t_паkv= 37,6 с.

Необходимые показатели качества были получены при значениях =10, ₁= 60

 

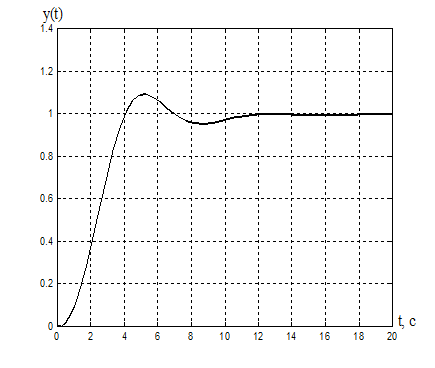
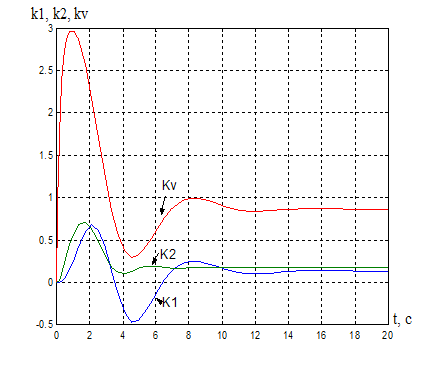
а)                                                                                           б)

Рисунок 7. а) Переходная характеристика адаптивной системы y(t): s% = 9%, = 6,2 с.

б)  Процессы на выходе адаптера:

k₁(t) =0,13,   t_паk1= 16,3 с;

k₂(t) =0,177,   t_паk2= 5,9 c;

k_V(t) =0,867,   t_паkv= 9,89 с.

7. Изменить начальные условия в объекте (,), получить вид y(t), , ,. Моделирование провести при  g==1, =1, =10.Сравнить с результатами   п.3.5.

а) g ==1

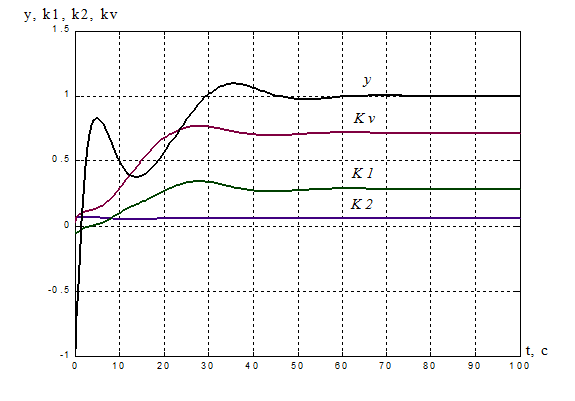
Рисунок 8. Переходная характеристика адаптивной системы y(t): s% = 9,5%, = 41,4 с.

 Процессы на выходе адаптера:

k₁(t) = 0.283,   t_паk1= 46,5 с;

k₂(t) = 0.0664,   t_паk2= 20,6 c;

k_V(t) =0.717,   t_паkv= 32,2 с.

б)=1, =10

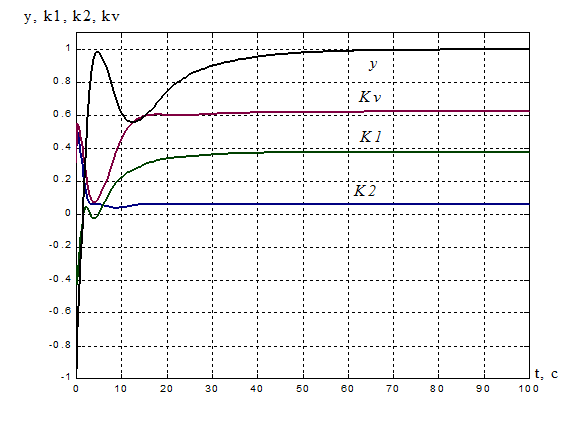
 Рисунок 9.  Переходная характеристика адаптивной системы y(t): = 38,6 с.

Процессы на выходе адаптера:

k₁(t) = 0.376,   t_паk1= 29,1 с;

 k₂(t) =0.0585,   t_паk2= 18,8 c;

k_V(t) =0.623,   t_паkv= 14,5 с.

Необходимые показатели качества были получены при значениях =15, ₁= 50

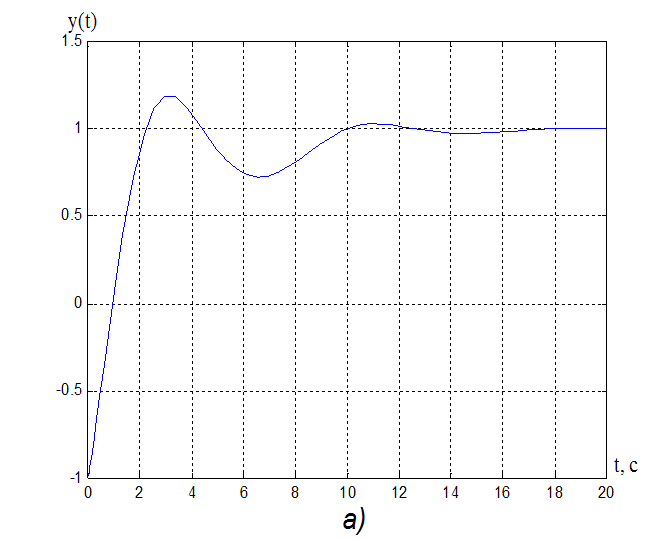
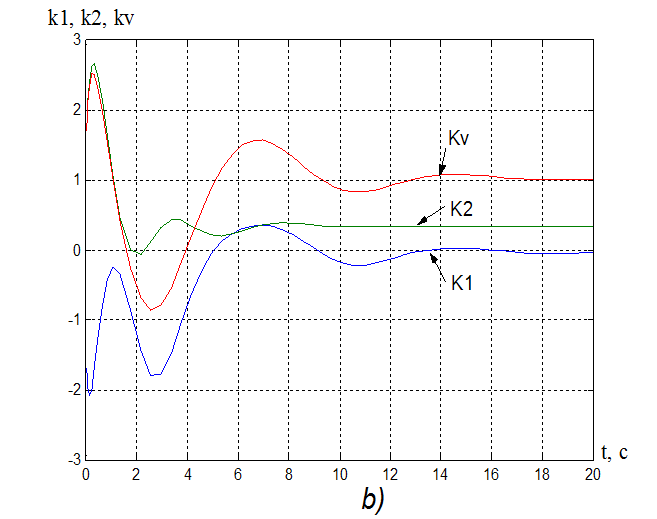
Рисунок 10. а) Переходная характеристика адаптивной системы y(t): s% = 18,5%, = 9,3 с.

б)  Процессы на выходе адаптера:

k₁(t) =-0,025,   t_паk1= 8,08 с;

k₂(t) =0,35,   t_паk2= 8,5 c;

k_V(t) =1,02,   t_паkv= 16 с.

7.* Изменить последовательно параметры объекта  в 2 раза,  выполнить п.3.5.

a) 2a₀

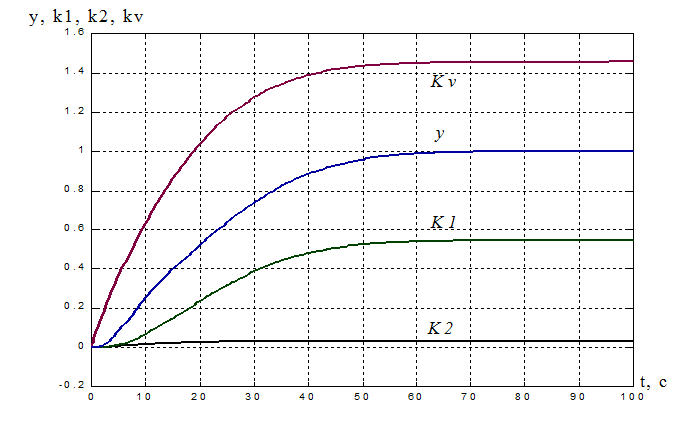
Рисунок 11.  Переходная характеристика адаптивной системы y(t): = 48.45 с.

Процессы на выходе адаптера:

k₁(t) = 0.545,   t_паk1= 48 с;

 k₂(t) =0.0344,   t_паk2= 30.95 c;

k_V(t) =1.455,   t_паkv= 39.3 с.

Необходимые показатели качества были получены при значениях =20, ₁= 50

 

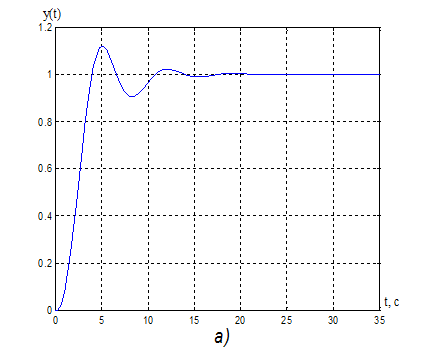
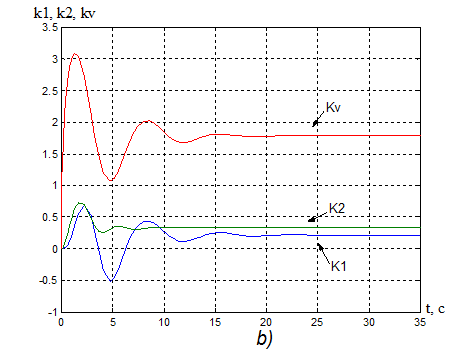
Рисунок 12. а) Переходная характеристика адаптивной системы y(t): s% = 12%, = 9,7 с.

б)  Процессы на выходе адаптера:

k₁(t) =0,22,   t_паk1= 20,1 с;

k₂(t) =0,33,   t_паk2= 7,6 c;

 k_V(t) =1,78,   t_паkv= 12,35 с.

б) 2a₁

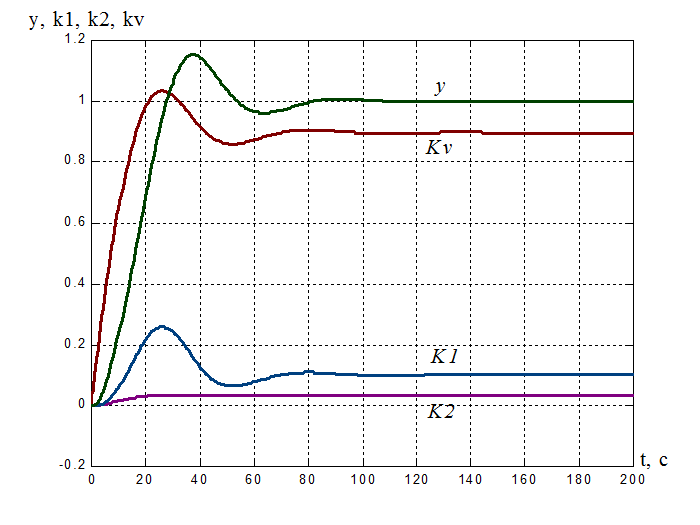
Рисунок 13.  Переходная характеристика адаптивной системы y(t): s% = 15,5%,= 48.83 с.

Процессы на выходе адаптера:

k₁(t) = 0.102,   t_паk1= 88,53 с;

 k₂(t) =0.0335,   t_паk2= 20,1 c;

k_V(t) =0,898,   t_паkv= 37,51 с.

Необходимые показатели качества были получены при значениях =20, ₁= 50

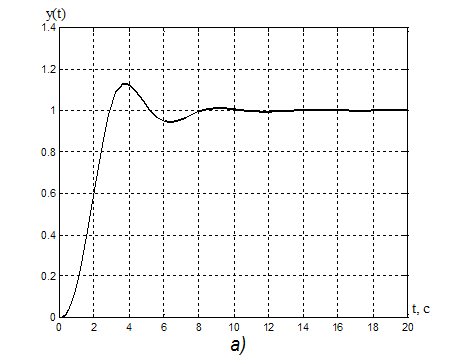
Рисунок 14. а) Переходная характеристика адаптивной системы y(t): s% = 16%, = 8,8 с.

б)  Процессы на выходе адаптера:

k₁(t) =-0,437,   t_паk1=11,75 с;

k₂(t) =0,3935,   t_паk2= 6,18 c;

k_V(t) =1,436,   t_паkv= 8,8 с.

в) 2b

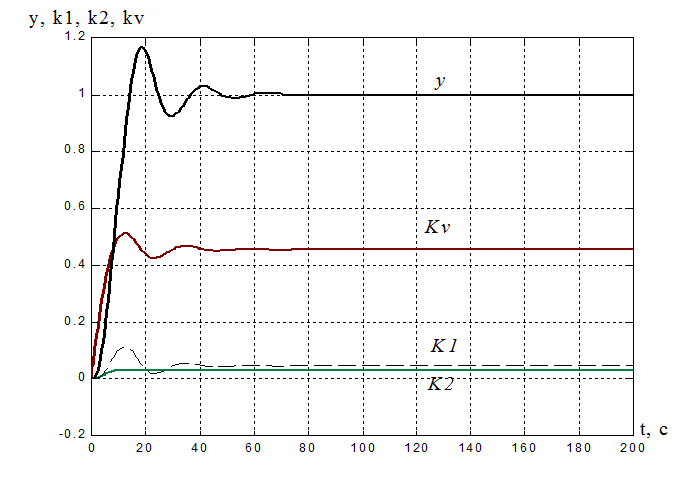
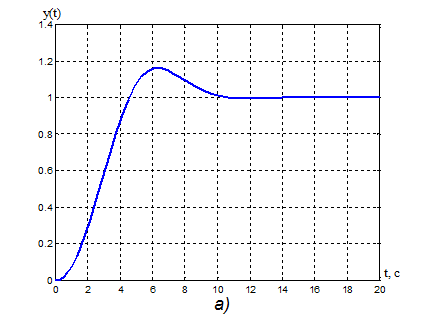
Рисунок 15.  Переходная характеристика адаптивной системы y(t): s% = 16,75%,= 32,8 с.

Процессы на выходе адаптера:

k₁(t) = 0.0447,   t_паk1= 50,45 с;

 k₂(t) =0.031,   t_паk2= 9,2 c;

k_V(t) =0,455,   t_паkv= 25,8 с.

Необходимые показатели качества были получены при значениях =20, ₁= 50

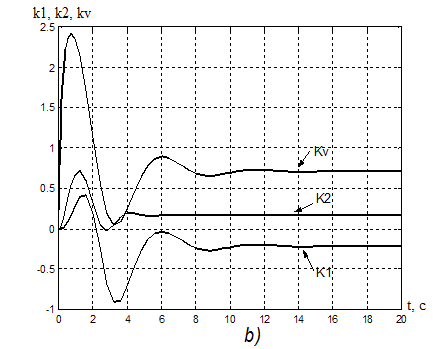
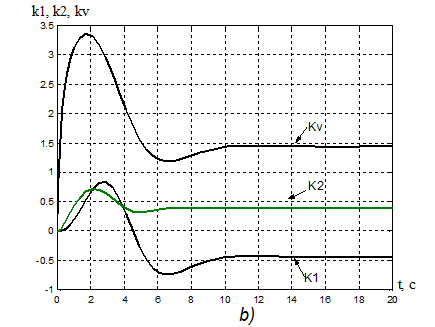
Рисунок 16. а) Переходная характеристика адаптивной системы y(t): s% = 13%, = 6,65 с.

б)  Процессы на выходе адаптера:

k₁(t) =-0,21,   t_паk1=12,05 с;

k₂(t) =0,171,   t_паk2= 5,87 c;

k_V(t) =0,71,   t_паkv= 9,5 с.

8.* Изменить модель объекта управления:  ,  (рисунок 1.2). Провести моделирование при нулевых начальных условиях и различных значениях :   а) =1, =1,   б) =1, =10,    в) =10, =1. Для улучшения процессов в системе изменить значения , . Сравнить с результатами  п.3.5.

а) =1, =1

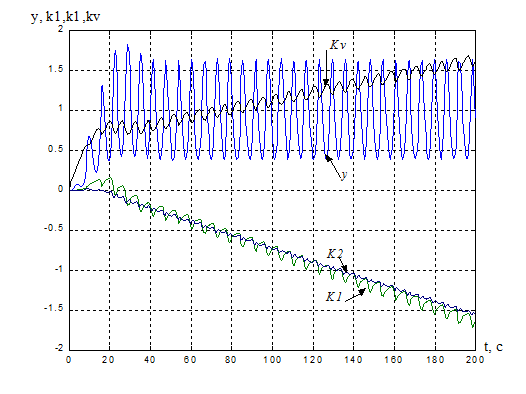
Рисунок 17.  Переходная характеристика адаптивной системы y(t) и процессы на выходе адаптера:  k₁(t),  k₂(t),  k_V(t).

Требуемые показатели качества были получены при значениях =900, ₁= 900

 

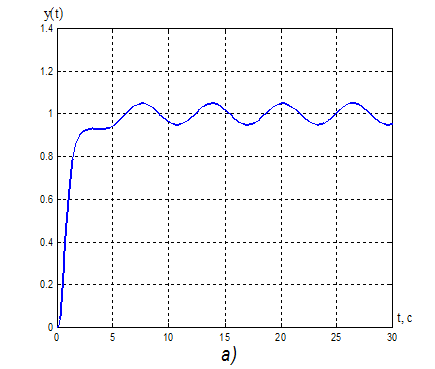
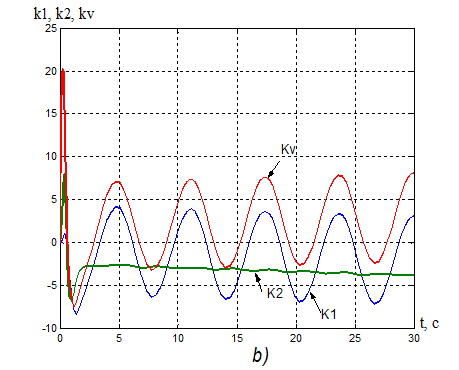
Рисунок 18. а) Переходная характеристика адаптивной системы y(t):  = 5,2 с.

б)  Процессы на выходе адаптера:  k₁(t),  k₂(t),  k_V(t).

б) =1, =10

Требуемые показатели качества были получены при значениях =20, ₁= 60

 

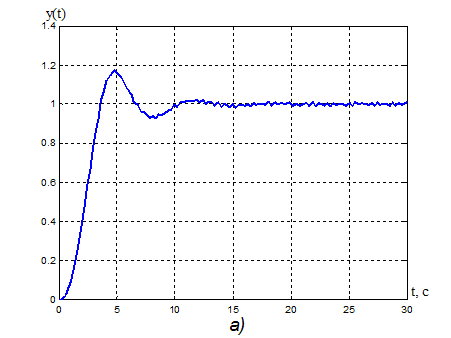
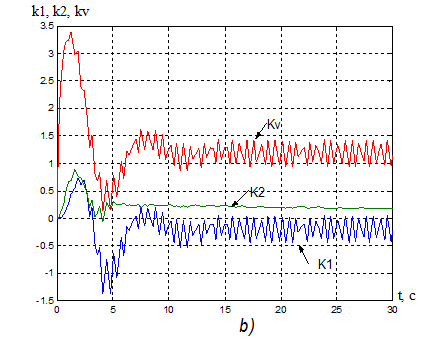
Рисунок 19. а) Переходная характеристика адаптивной системы y(t):  s% = 17,5%, = 8,9 с.

б)  Процессы на выходе адаптера:  k₁(t),  k₂(t),  k_V(t).

в) =10, =1

Требуемые показатели качества были получены при значениях =8500,  ₁= 9000

 

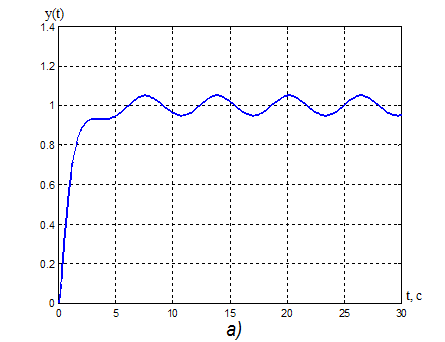
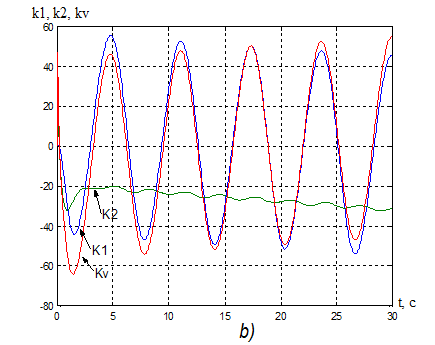
Рисунок 20. а) Переходная характеристика адаптивной системы y(t):  = 5,2 с.

б)  Процессы на выходе адаптера:  k₁(t),  k₂(t),  k_V(t).