Исследование системы поиска экстремума с синхронным детектированием (Лабораторная работа № 1), страница 3

          4.5. При  исследовать влияние начальных условий ФОЧП на y(t), Y(t) и G(t), изменяя  в диапазоне (0,6 - 5) .

          4.6. Исследовать влияние параметра с на характер процессов, уменьшая и увеличивая его значение в 5 раз при исходных значениях начальных условий ДФ и ФОЧП. Сравнить результаты с процессами, полученными в п.4.1. Зарисовать переходные процессы y(t), Y(t) и G(t).

          4.7. При  и  исследовать влияние m на y(t), Y(t) и G(t), уменьшая его значение в 5 раз относительно расчетного.

          4.8. При  и  оценить влияние m₁ на процессы в системе, уменьшая его значение в 5 раз относительно m₂.

          4.9. При  и  и  рассчитанном  значении  m₂ проанализировать влияние m₁ на y(t), Y(t) и G(t), уменьшая его значение в 5 раз относительно m₂.

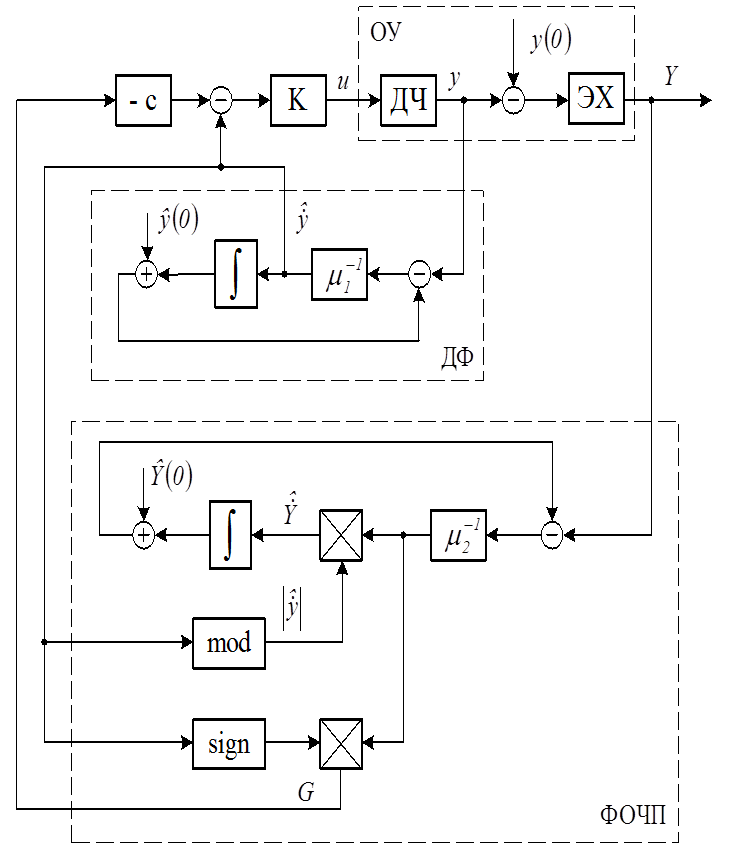
Рис.2.1. Структурная схема системы поиска экстремума

5. Содержание отчета

          5.1. Цель работы.

          5.2. Результаты расчета параметров регулятора, фильтра оценки частной производной и дифференцирующего фильтра.

          5.3. Структурная схема системы.

          5.4. Графики всех переходных процессов и фазовых портретов.

5.5. Выводы по работе.

6. Контрольные вопросы

          6.1. Как формируется закон управления в системах, основанных на принципе локализации?

          6.2. Какова роль градиента в системах подобного типа?

          6.3. С какой целью в систему вводится дифференцирующий фильтр?

          6.4. Как оценить градиент с помощью ФОЧП?

          6.5. Какое влияние оказывают малые инерционности фильтров на свойства замкнутой системы?

Лабораторная работа №3

ИССЛЕДОВАНИЕ свойств ОПТИМАЛЬНОЙ

ПО БЫСТРОДЕЙСТВИЮ СИСТЕМЫ

1.  Цель работы

Знакомство с принципом построения оптимальных и субоптимальных систем, анализом влияния основных параметров на ее переходные процессы и фазовый портрет.

2.  Основные сведения

В работе исследуется объект управления, математическая модель которого имеет вид

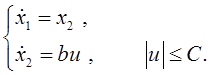                                                  (3.1)

Требуется обеспечить в замкнутой системе оптимальные по быстродействию процессы перехода из произвольного начального состояния {x₁(0), x₂(0)} в заданное конечное, которое совпадает с началом координат, т.е. {x₁(T)=0, x₂(T)=0}.

С этой целью формируется оптимальный закон управления

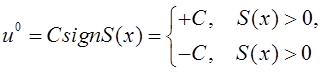(3.2)

где S(x) – линия переключения управляющего воздействия, которая описывается уравнением

                                   (3.3)

b

          Структурная схема оптимальной по быстродействию системы приведена на рис.3.1.

 

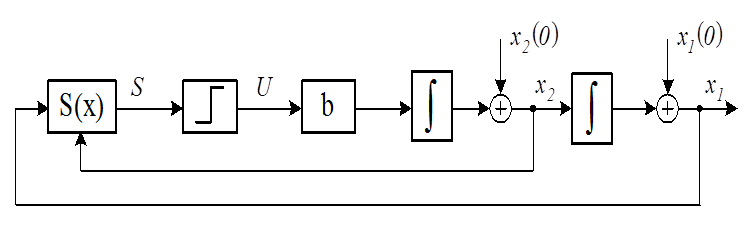
Рис.3.1. Структурная схема оптимальной по быстродействию системы

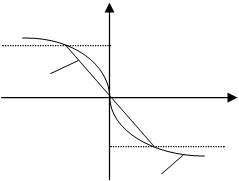
          В реальных системах точно реализовать полученную линию переключения не удается, поэтому используют ее различные аппроксимации, простейшей из которых является аппроксимация прямыми линиями (рис.3.2).

                 x₂

                D

S_p(X) = 0

                                      x₁

          -D

                               S(X) = 0

            Рис.3.2. Аппроксимация линии переключения

          Реальный алгоритм управления по форме совпадает с (3.2), но вместо S(x) используется ее аппроксимация S_p(x).

          В этом случае получают не оптимальные, а близкие к ним процессы, которые называются субоптимальными.

3.Методические указания

          3.1. При моделировании процессов с помощью программы “Компас” для получения модуля сигнала используется звено “ВЫПР”.

          3.2. В качестве метода интегрирования рекомендуется выбирать метод Рунге – Кутта 4-го порядка, а предлагаемый шаг интегрирования уменьшить в 10 раз.