Министерство Образования и Науки Российской Федерации
Федеральное агентство по образованию
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра Автоматики
Лабораторная работа №1
система с градиентным алгоритмом адаптации
Вариант №5
Студент: Овченков Д.В.
Дата выполнения: ………………………
Отметка о защите: ………………………
1. Цель работы
Изучение свойств системы с алгоритмом адаптации, синтезированным по градиентному методу, анализ влияния темпа параметрических возмущений на качество процессов и величину управляющего воздействия.
2. Исходные данные
|
Коэффициенты ОУ |
Перерегулирование, σ% |
Время переходного процесса, tп |
||
|
a0 |
a1 |
b |
||
|
0.1 |
0.5 |
0.1 |
30 |
10 |
Объект управления имеет математическую модель вида:
![]() = A x +
B u, y = C x, (2.1)
= A x +
B u, y = C x, (2.1)
где ![]() - вектор координат
состояния, y - выходная переменная, u - управляющее воздействие, y, uÎ
- вектор координат
состояния, y - выходная переменная, u - управляющее воздействие, y, uÎ ![]() ; A, B, C - матрицы коэффициентов соответствующих
размерностей;
; A, B, C - матрицы коэффициентов соответствующих
размерностей;
A=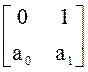 , B=
, B=![]() , C=
, C=![]() ,
(2.2)
,
(2.2)
![]() ,
, ![]() ,
b- неизвестные коэффициенты, которые
могут быть как постоянными, так и переменными. Желаемое поведение системы
описывают уравнения эталонной модели:
,
b- неизвестные коэффициенты, которые
могут быть как постоянными, так и переменными. Желаемое поведение системы
описывают уравнения эталонной модели:
![]()
![]() ,
(2.3)
,
(2.3)
где r- входная переменная,
![]() =
=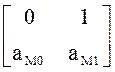 ,
, ![]() =
=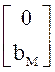 ,
, ![]() =
=![]() .
.
Закон управления формируется в виде:
![]()
или ![]() . (2.4)
. (2.4)
Коэффициенты регулятора изменяются по градиентному алгоритму
адаптации: ![]() ,
,
![]() ,
(2.5)
,
(2.5)
![]() ,
,
![]() .
.
3. Ход работы
3.1 Расчет параметров адаптивного регулятора и наблюдателя
Определение элементов матриц ![]() ,
,
![]() ,
, ![]() по
заданным требованиям к качеству процессов (таблица 1):
по
заданным требованиям к качеству процессов (таблица 1):
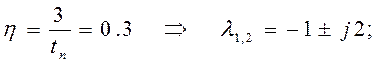
![]()
![]()
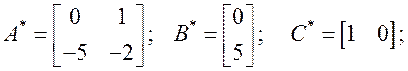
![]() .
.
Расчет наблюдателя:
![]() ;
;
![]() ;
;
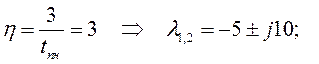
![]() ;
;
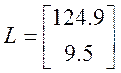 .
.
Уравнение системы с наблюдателем и вычисленными параметрами:
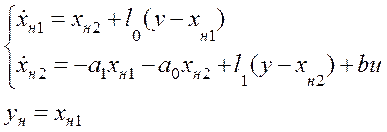
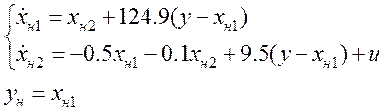
3.2. Выполнить моделирование стационарного и
нестационарного объектов (![]() =10,
=10, ![]() =1), оценить устойчивость, определить
показатели качества( σ %, tn ).
=1), оценить устойчивость, определить
показатели качества( σ %, tn ).
Стационарный объект управления:
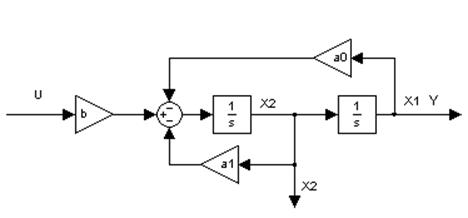
у
 t
t
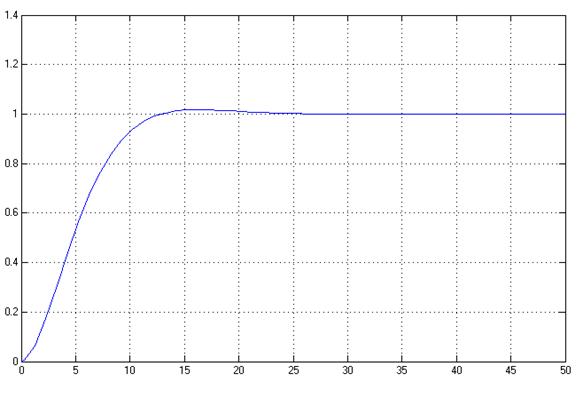
Рис. 1. Переходный процесс y(t). Стационарный объект (% = 1%, tпп = 10,5 с)
Нестационарный объект управления:
у
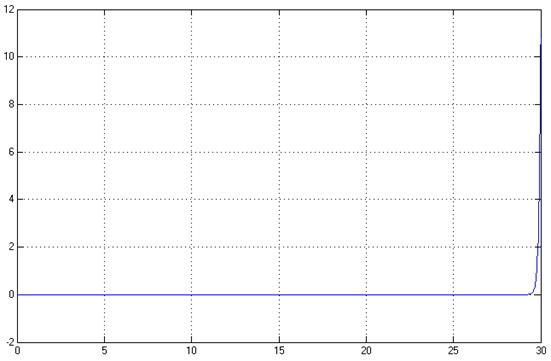 t
t
Рис. 2. Переходный процесс y(t). Нестационарный объект, система неустойчива.
3.3. Собрать схему эталонной модели на интегрирующих элементах. Получить переходную характеристику (r=1(t), x1(0)=x2(0)=0). Определить показатели качества( σ %, tn ).
y
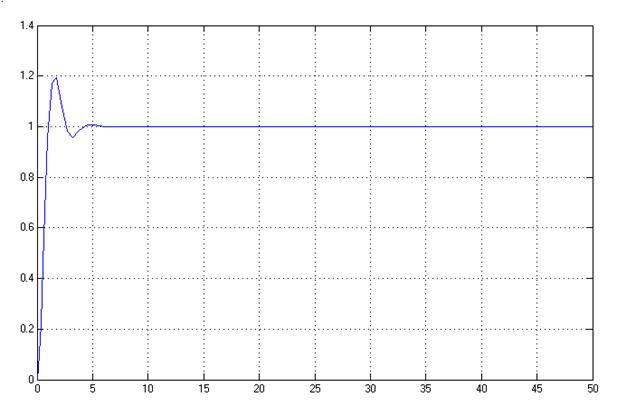 t
t
Рис. 3. Переходный процесс в эталонной модели (% = 19.5%, tпп = 2.4 с)
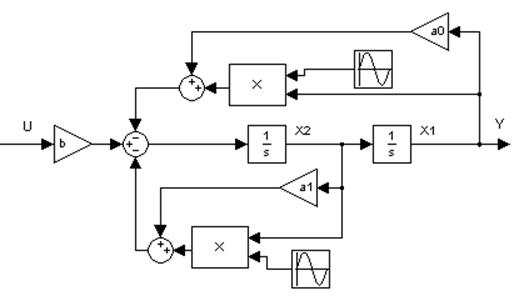
3.4. Собрать схему адаптивной системы (2.1), (2.3)-(2.5). Параметры объекта управления приведены в таблице 1.
Структурная схема адаптивной системы:
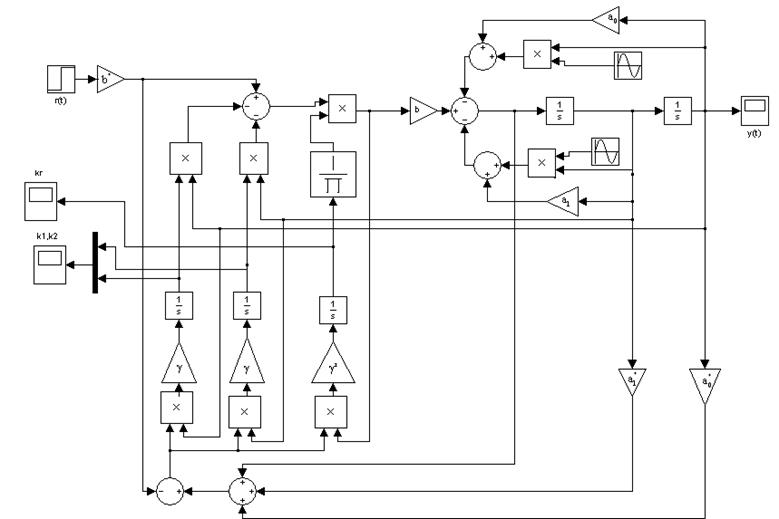
3.5.
Получить графики переходной характеристики
системы (y(t)), управляющего воздействия и процессов на выходе
адаптера (![]() ) при r(t)=1(t), нулевых начальных условиях, кроме
) при r(t)=1(t), нулевых начальных условиях, кроме ![]() , γ=1.
, γ=1.
![]()
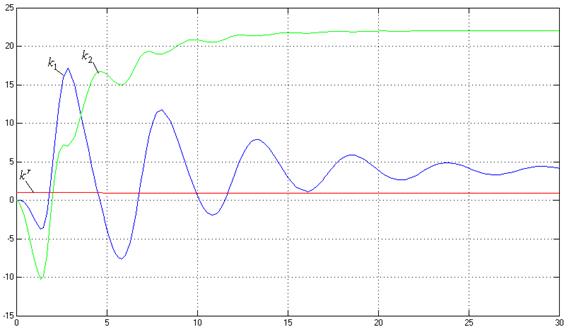 t
t
Рис. 4. Переходные
процессы ![]()
y
 t
t
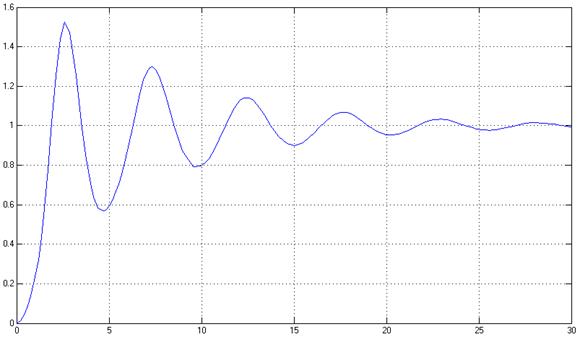
Рис. 5. Переходный процесс системы при γ = 10, 10, 0,001. Полученные показатели качества не удовлетворяют желаемым.
3.6. Определить показатели качества, сравнить их значения с заданными. Если качество процесса неудовлетворительное, то изменяя γ, добиться достижения требуемых показателей.
y
 t
t
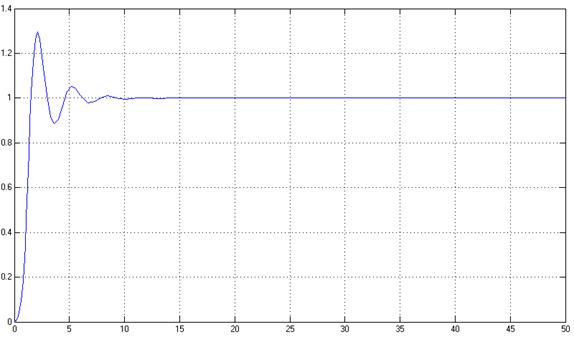
Рис. 6. Переходный процесс системы СС (% = 29,5%, tпп = 5,2 с)
γ = 50, 50, 0,001. Полученные показатели качества удовлетворяют желаемым.
3.7. Изменить начальные условия в объекте (![]()
![]() ), получить вид y(t),
), получить вид y(t), ![]() (t),
(t),
![]() (t),
(t), ![]() (t), u
(t).
Моделирование провести для различных значений g. Сравнить с
результатами п.3.5. Изобразить зависимость γ от x1(0) при γr=0.001 и x2(0)=0
(t), u
(t).
Моделирование провести для различных значений g. Сравнить с
результатами п.3.5. Изобразить зависимость γ от x1(0) при γr=0.001 и x2(0)=0
y
 t
t
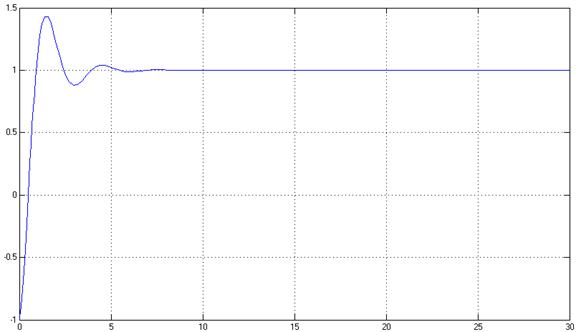
Рис.7. Переходный процесс системы, y(t) при γ=100 (% = 42%, tпп = 3,6 с).
U
 t
t
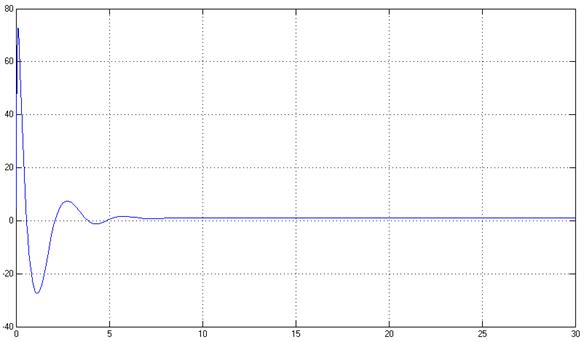
Рис. 8. Управляющее воздействие, U(t) при γ=100
![]()
 t
t
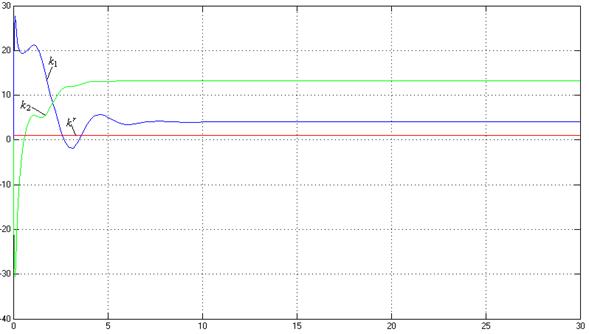
Рис. 9. Процессы на
выходе адаптера (![]() ,
,![]() ) при γ=100 .
) при γ=100 .
y
 t
t
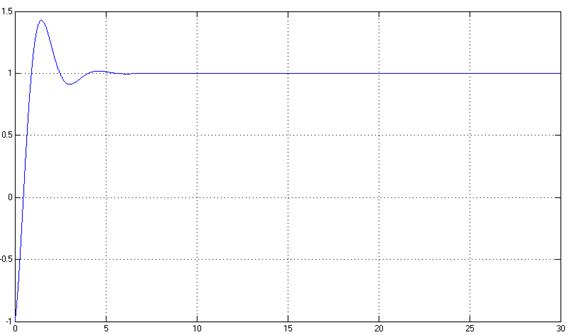
Рис.10. Переходный процесс системы, y(t) при γ=10000 (% = 42%, tпп = 3,6 с).
U
 t
t
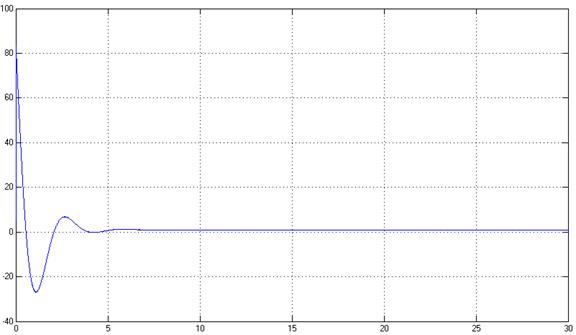
Рис. 11. Управляющее воздействие, U(t) при γ=10000
![]()
 t
t
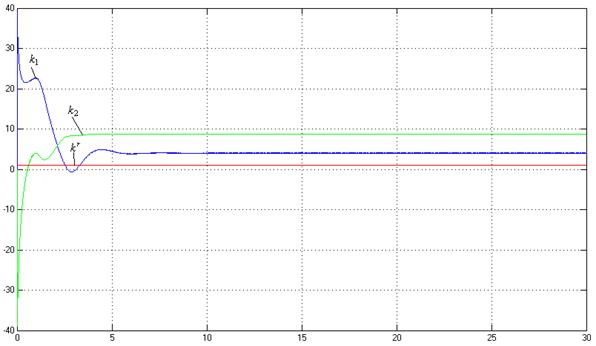
Рис. 12. Процессы на выходе адаптера (![]() ,
,![]() ) при γ=10000 .
) при γ=10000 .
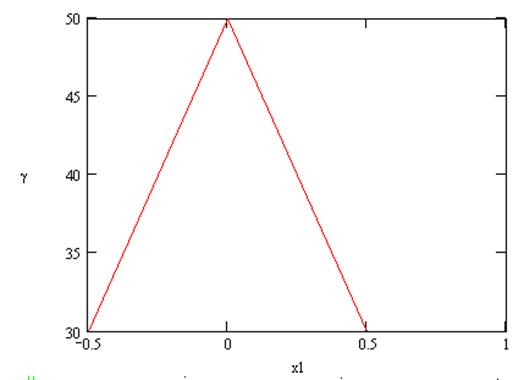
Рис. 13. Зависимость γ от x1(0) при γr=0.001 и x2(0)=0
3.8 Изменить модель
объекта управления, ![]() ,
, ![]() .
Провести моделирование адаптивной системы при нулевых начальных условиях,
кроме
.
Провести моделирование адаптивной системы при нулевых начальных условиях,
кроме ![]() (0) ≠ 0,
(0) ≠ 0, ![]() (0) = 1,
и различных значениях
(0) = 1,
и различных значениях ![]() ,
, ![]() : а)
: а) ![]() =1,
=1, ![]() =1, б)
=1, б)
![]() =1,
=1, ![]() =10, в)
=10, в)
![]() =10,
=10, ![]() =1. Для
улучшения процессов в системе изменить значения γ в 10 раз. Сравнить с результатами
п.3.5.
=1. Для
улучшения процессов в системе изменить значения γ в 10 раз. Сравнить с результатами
п.3.5.
а) ![]() =1,
=1,
![]() =1 γ=100
=1 γ=100
y
 t
t
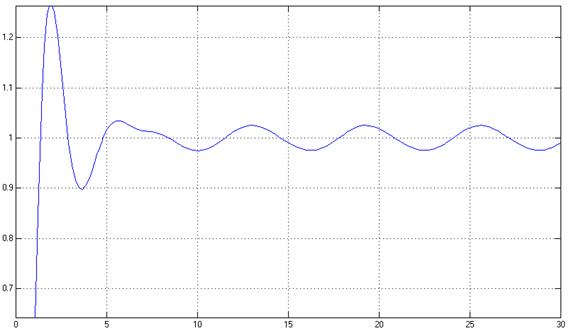
Рис. 14. Переходный процесс в системе, y(t).
Показатели качества системы удовлетворяют требуемым.
![]()
 t
t
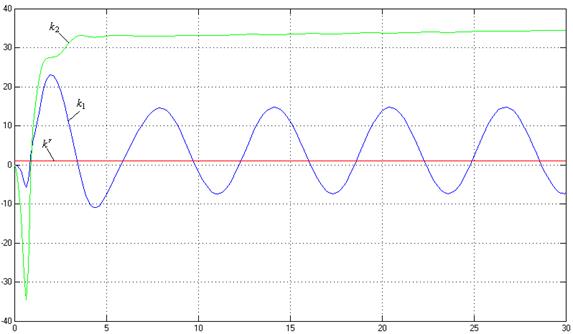
Рис.15. Процессы на выходе адаптера (![]() ,
,![]() ).
).
U
 t
t
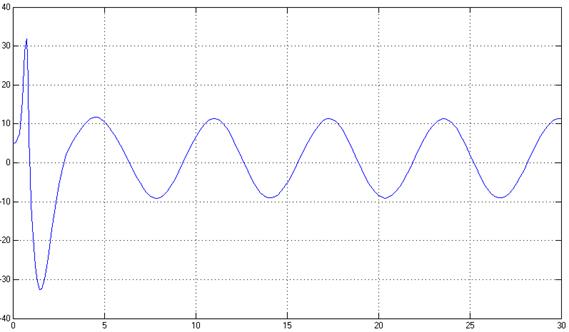
Рис.16. Управляющее воздействие, U(t)
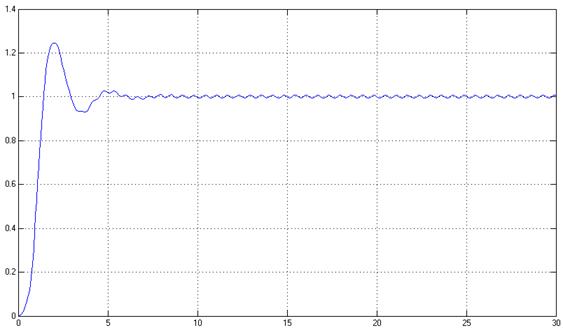
б) ![]() =1,
=1,
![]() =10, γ=100
=10, γ=100
y
 t
t
Рис. 17. Переходный процесс в системе, y(t)
Показатели качества системы удовлетворяют требуемым.
![]()
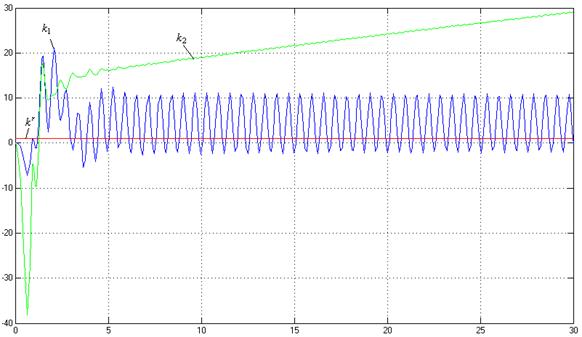 t
t
Рис.18. Процессы на выходе адаптера (![]() ,
,![]() ).
).
U
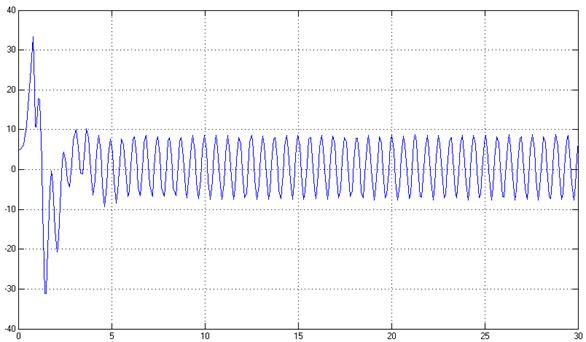 t
t
Рис.19. Управляющее воздействие, U(t)
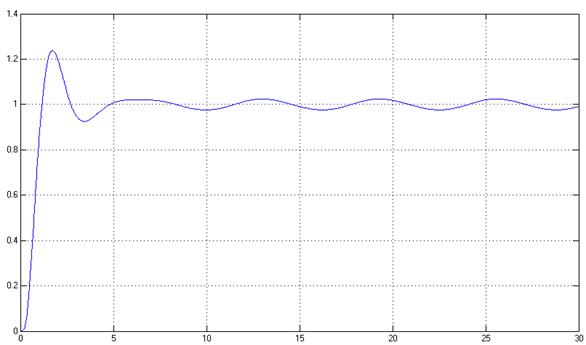
в) ![]() =10,
=10,
![]() =1, γ=1000
=1, γ=1000
y
 t
t
Рис.20. Переходный процесс в системе, y(t)
Показатели качества системы удовлетворяют требуемым.
![]()
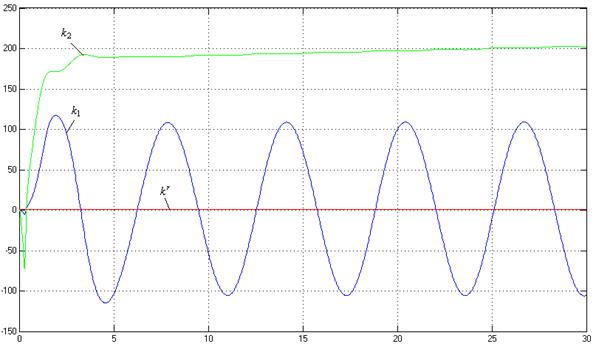 t
t
Рис.21. Процессы на выходе адаптера (![]() ,
,![]() ).
).
t
U
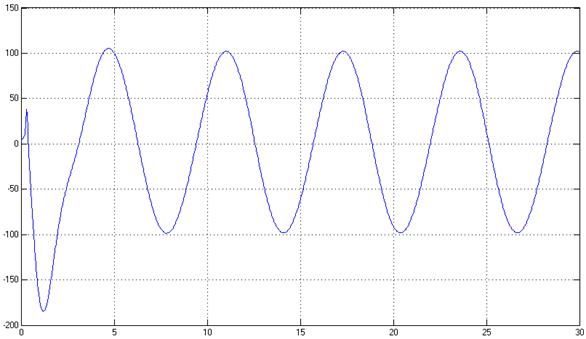 t
t
Рис.22. Управляющее воздействие, U(t)
3.9 Рассчитать параметры наблюдателя. Собрать схему системы с наблюдателем. Повторить пп. 3.4, 3.8
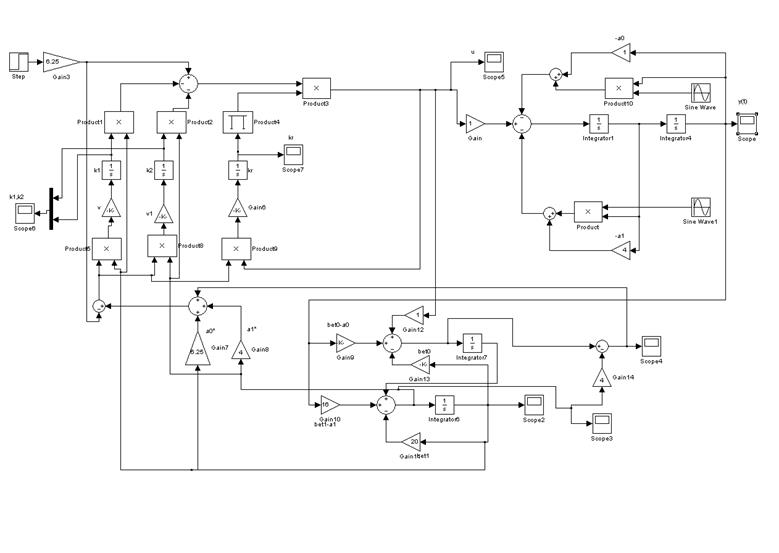
Структурная схема системы с наблюдателем:
а) ![]() =1,
=1,
![]() =1, γ=200
=1, γ=200
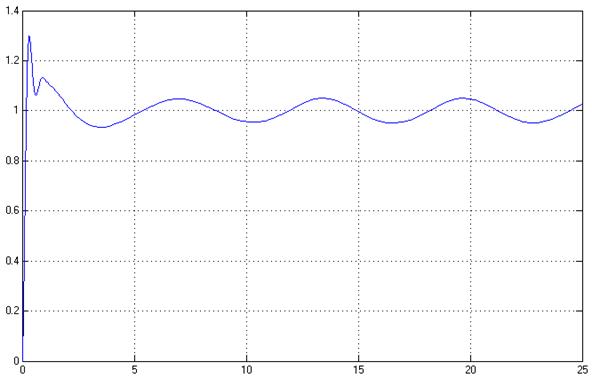
Рис.23. Переходный процесс в системе, y(t)
Показатели качества системы удовлетворяют требуемым
![]()
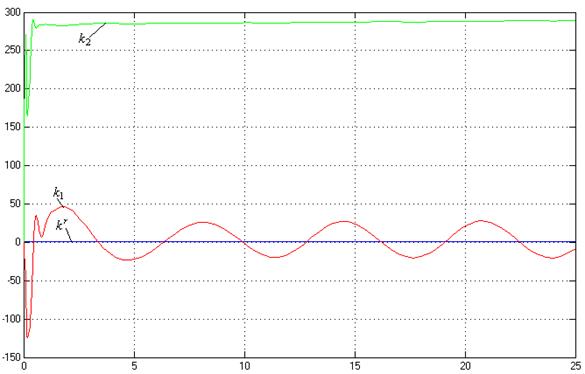
Рис.24. Процессы на
выходе адаптера (![]() ,
,![]() ).
).
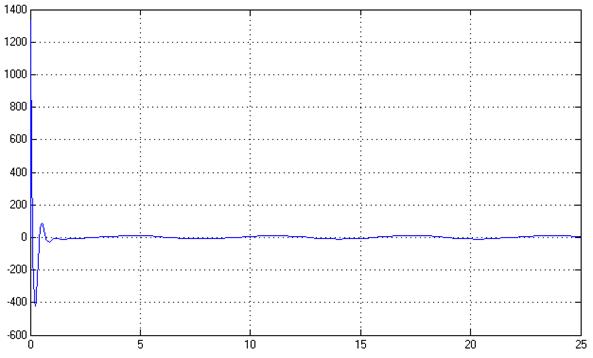
Рис.25. Управляющее воздействие, U(t)
б) ![]() =1,
=1,
![]() =10, γ=70
=10, γ=70
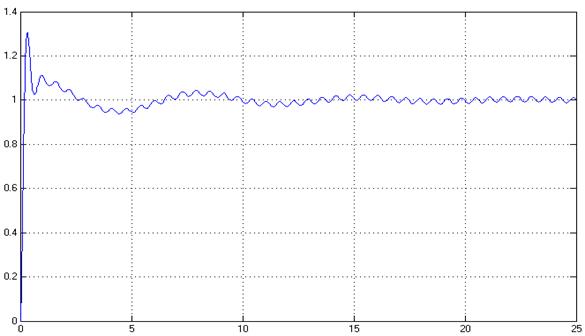
Рис.26 Переходный процесс в системе, y(t)
Показатели качества системы удовлетворяют требуемым.
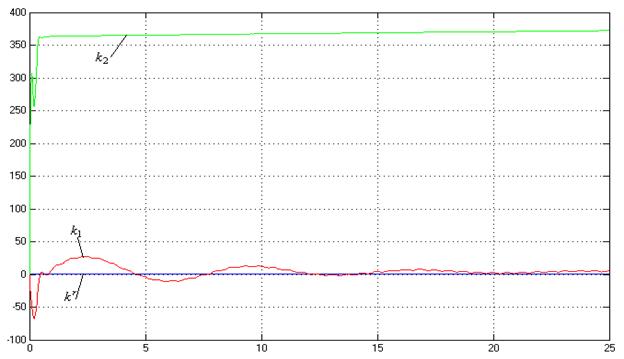
Рис.27. Процессы на
выходе адаптера (![]() ,
,![]() ).
).
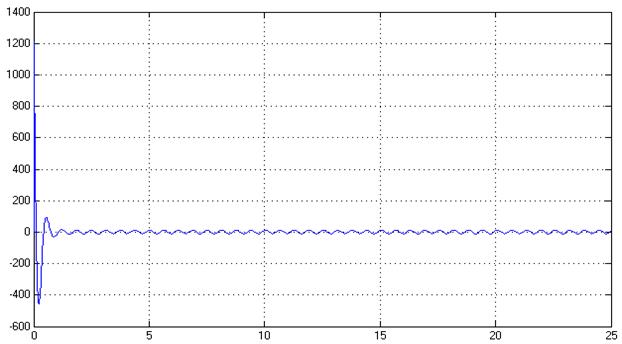
Рис.28. Управляющее воздействие,U(t)
в) ![]() =10,
=10,
![]() =1, γ=400
=1, γ=400
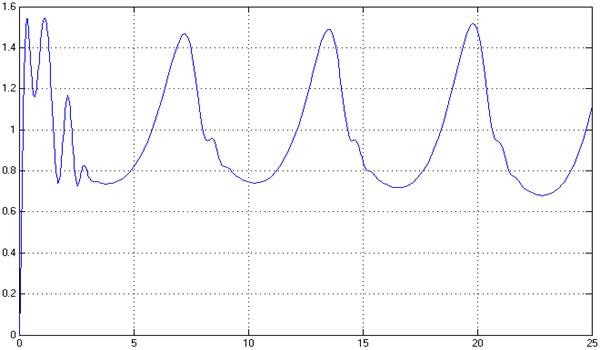
Рис.29. Переходный процесс в системе, y(t)
Показатели качества системы не удовлетворяют требуемым.
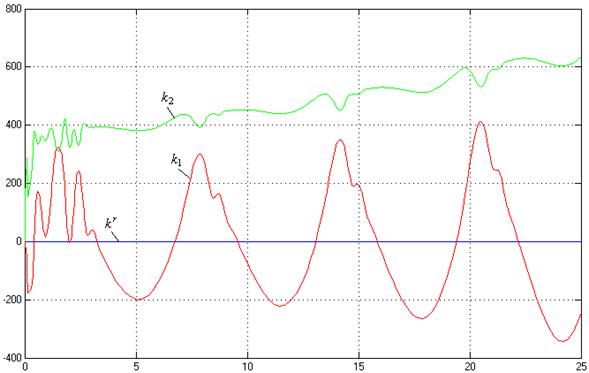
Рис.30. Процессы на
выходе адаптера (![]() ,
,![]() ).
).
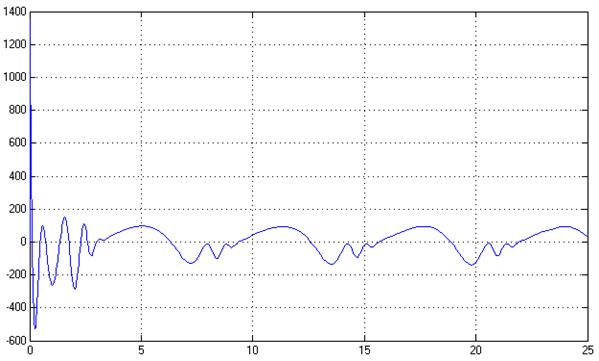
Рис.31. Управляющее воздействие,U(t)
Вывод
С помощью градиентного алгоритма адаптации получили систему с разными показателями качества переходного процесса. При не нулевых начальных условиях не возможно было получить требуемых показателей качества, даже при подборе коэффициента γ.
Параметрические возмущения влияют на качество процессов следующим образом:
-
увеличение
амплитуды ![]() приводит к росту управляющего воздействия
и показатели качества переходного процесса становятся неудовлетворительными;
приводит к росту управляющего воздействия
и показатели качества переходного процесса становятся неудовлетворительными;
- с ростом частоты параметрических колебаний показатели качества переходного процесса становятся лучше.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.