Статистическое моделирование. Построение статистических рядов и функций, страница 6

     Если моделируемая случайная величина непрерывная, то для неё строят интервальный статистический ряд. Сначала находят число интервалов r, на которые разбивается отрезок , где через  и  обозначены наименьшее и наибольшее выборочные значения. Число r вычисляют   по следующей формуле:

                                      ,

где через  обозначена  целая часть .

     Границы  интервалов находят по формулам: 

                       ·   ,  , 

                       ·    , 

                        ·   .

     Составляют интервальный статистический ряд:

                                  ...                 

        ·                      ...            ,        ,       .

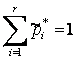     В приведенных формулах через  обозначено число выборочных значений, попавших в i-ый интервал J_i (частота попадания выборочных значений в интервал с номером i, i=1,…,r), а через  обозначена относительная частота.

 Число интервалов r, на которые разбивается отрезок , может выбираться произвольно, а не по указанной формуле, главное чтобы оно находилось в диапазоне   от пяти до двадцати пяти.

В качестве замечания следует отметить, что если выборка значений случайной дискретной величины очень большая, то ее значения также группируют в виде интервального ряда.

Эмпирическую функцию распределения , которая служит оценкой теоретической функции распределения F_ξ (x), определяют следующим образом:

Для  непрерывной величины    для  дискретной величины

    

                                                                                                                         

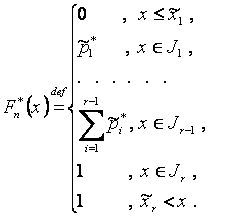
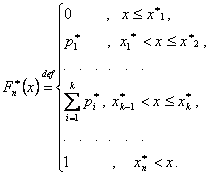
          При построении кумуляты (графика эмпирической функции распределения) случайной дискретной величины строят график кусочно-постоянной функции . Для случайной непрерывной величины строят график в виде непрерывной ломаной следующим образом: