Геометрическое распределение характеризуется только одним параметром: вероятностью появления случайного события А в одном испытании Р(А)=р. Поэтому для обозначения, чтоξ распределена по геометрическому закону с параметром р следующее: ξÎG(р).
Математическое ожидание и дисперсию случайной величины, распределенной по геометрическому закону, через его параметр можно вычислить по формулам:
·Е[ξ]=![]() , V[ξ]=
, V[ξ]=![]() .
.
·Непрерывная случайная величина равномерно распределена на отрезке [a,b], если выражение для плотности распределения имеет вид:

У этого распределения два параметра: границы отрезка а и b. Символьное обозначение того, что случайная величина ξ распределена по равномерному закону с параметрами а и bследующее: ξÎR(а, b).
Функция распределения случайной величины, равномерно распределенной на отрезке [a,b], определяется выражением:

Математическое ожидание и дисперсия случайной величины, равномерно распределенной на отрезке [a,b], могут быть вычислены через параметры этого распределения по формулам:
·Е[ξ]=
![]() , V[ξ]=
, V[ξ]=![]() .
.
·Плотность распределения показательно распределенной случайной величины с параметром l>0 задается следующей функцией:
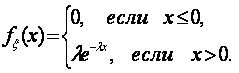
Выражение для функции распределения показательно распределенной случайной величины следующее:
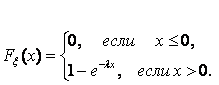
Формулы, связывающие математическое ожидание и дисперсию показательно распределенной случайной величины и параметр l этого распределения следующие:
![]() · Е[ξ]=
· Е[ξ]=
![]() , V[ξ]=
, V[ξ]=![]() .
.
Символьное обозначение того, что случайная величина ξ распределена по показательному закону распределения с параметром lследующее: ξÎЕ(l).
·Одним из важнейших непрерывных распределений является нормальное (гауссовское) распределение случайной величины, которое характеризуется двумя параметрами: mÎR и s> 0.
Плотность нормально распределенной случайной величины имеет вид:
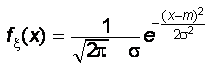 .
.
Функция плотности не интегрируема в классе элементарных функций, поэтому выражение для функции распределения имеет вид:
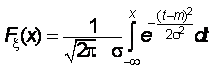 .
.
С нормальным распределением связано понятие функции Лапласа Ф(х), определяемой следующим образом:
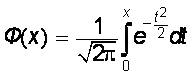 .
.
Функция
распределения ![]() и функция Лапласа Ф(х)
связаны равенством:
и функция Лапласа Ф(х)
связаны равенством:
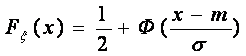 .
.
·Вероятность попадания нормально распределенной случайной величины в промежуток <a, b> вычисляется по формуле:
![]() .
.
Если параметры m=0 и s=1, то распределение называют стандартным нормальным распределением.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.