Статистическое моделирование. Построение статистических рядов и функций, страница 24

     На практике большой интерес вызывают задачи сравнения двух выборок, в частности, одним из основных вопросов, является вопрос, извлечены ли эти выборки из одной и той же генеральной совокупности. Так, например, если есть основания считать, что обе выборки извлечены из нормально распределенной генеральной совокупности, то для ответа на поставленный вопрос остается проверить, одинаковые ли параметры этих распределений.

     Пусть имеются две выборки нормально распределенных случайных величин с параметрами m₁=E[ξ₁]  , s₁²=V[ξ₁] и m₂=E[ξ₂]  , s₂²=V[ξ₂]. Для каждой случайной величины по имеющимся выборкам объемов n₁ и n₂ соответственно, вычисляют выборочные средние и выборочные дисперсии: и   , анализируют полученные  результаты и выдвигают  гипотезы:

                                                     H₀: m₁=m₂,

                                                     H_a: m₁¹m₂,

а затем следующие  гипотезы:               

                                                     H₀: s₁²=s²₂,

                                                     H_a: s₁²¹s²₂.

     Для проверки первой группы гипотез о равенстве математических ожиданий вычисляют выборочную статистику вида:

                        ·              .

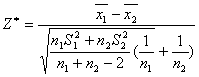     При справедливости основной гипотезы о равенстве средних значений эта случайная величина будет иметь распределение Стьюдента с n₁+n₂-2 степенями свободы. Критическая область, при сформулированной альтернативной гипотезе, будет двусторонней. Ее границы ищут по таблицам критических точек распределения Стьюдента (двусторонних) по заданному уровню значимости 1-α и  n₁+n₂-2 числу степеней свободы.Если выборочная статистика удовлетворяет неравенству к₁<Z^*<к₂, то принимают основную гипотезу о равенстве средних, если не удовлетворяет, то принимают альтернативную гипотезу о том, что они не равны.

       Чтобы проверить гипотезу о равенстве дисперсий, составляют следующую вспомогательную случайную величину:

                                      ·       ,

где через S²_max обозначена большая из выборочных дисперсий  S₁² и S₂²,  а через S_min²- меньшая.

     Если основная гипотеза о равенстве дисперсий справедлива, то вспомогательная случайная величина Z^* распределена по закону Фишера с n₁-1 , n₂-1 степенями свободы. Критическая область будет правосторонней, ее границу ищут по таблицам распределения Фишера по заданному уровню значимости и n₁-1 , n₂-1 степеням свободы. Если 0 < к₁<Z^*<к₂, то принимают основную гипотезу о равенстве дисперсий,если выполняется неравенство

Z^* > к₂, то основную гипотезу отклоняют в пользу альтернативной.