Статистическое моделирование. Построение статистических рядов и функций, страница 20

 Обычно гипотеза о виде закона распределения выдвигается после визуального изучения кумуляты, гистограммы и анализа полученных оценок числовых характеристик.

     При проверке основной гипотезы  с использованием критерия Пирсона для случайной дискретной величины сначала составляют сгруппированный статистический ряд, а затем вычисляют следующую выборочную статистику:

                                     ·      .

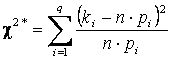В  формуле для  n это объем выборки, k_i это частота выборочного значения ,  это теоретические вероятности, которые вычисляются исходя из предположения о виде закона распределения (гипотезы ).

Для случайной непрерывной величины сначала строят интервальный статистический ряд, а затем вычисляют выборочную статистику по следующему  правилу:

                            ·             .

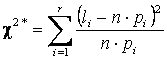Здесь li это частота попадания выборочного значения в интервал с номером i.  Вероятности попадания случайной непрерывной величины в интервал с номером i  , вычисляются по одной из двух формул:

·                      или       ·        .

 

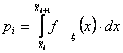Здесь             -       гипотетические функция распределения и гипотетическая плотность соответственно.

При проверке гипотез по критерию Пирсона критическая область будет правосторонней. Её границу к₂ ищут по таблицам распределения  по заданному уровню значимости  и  степенями свободы из условия . Для  случайной дискретной величины число степеней свободы будет равно: , для случайной непрерывной -- , где  - число параметров распределения, оцениваемых по выборке.

Например, если случайная величина распределена по нормальному закону, то у этого распределения два параметра m=E[ξ]  и s²=V[ξ]. В том случае, если оба параметра оценивались по выборке, s=2. У случайной величины,     распределенной по      показательному     закону,  один параметр

λ=1/ E[ξ] , поэтому  , s=1, если этот параметр оценивался с использованием выборочной информации. Равномерный закон распределения на отрезке [а, в] характеризуется двумя параметрами: границами этого отрезка, значит, если они оценивались по выборке,  то s=2.

Если , то гипотеза  принимается, если  основная гипотеза отвергается.

Следует обратить внимание на то, что при проверке гипотезы по критерию Пирсона для случайной непрерывной величины, в случае если частота попадания в интервал  , следует объединить интервал  с любым соседним.

При проверке гипотезы о виде закона распределения случайной непрерывной величины по критерию согласия Колмогорова  вычисляют следующую выборочную статистику