Статистическое моделирование. Построение статистических рядов и функций, страница 23

                   6.2 Проверка параметрических гипотез

      Параметрические гипотезы несут в себе суждения о параметрах распределения. Как уже отмечалось, параметры распределения зачастую связаны с числовыми характеристиками, поэтому для нормального закона проверка гипотез о параметрах распределения  сводится к проверке гипотез о числовых характеристиках.

     Предположим, что изучаемая случайная величина распределена по нормальному закону с параметрами m=E[ξ]  и s²=V[ξ], которые нам неизвестны.  Располагая выборочными данными можно вычислить оценки этих параметров  и S²  и выдвинуть предположение о том, чему равно неизвестное математическое ожидание, то есть:

                                                     H₀: m=m₀,

                                                     H_a: m¹m₀.

     Для проверки сформулированной гипотезы вычисляют выборочную случайную величину по формуле:

                                          ·       .

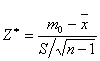     Если основная гипотеза Н₀ верна, то указанная случайная величина распределена по закону Стьюдента с n-1 степенью свободы. Поэтому по таблицам распределения Стьюдента, или при помощи функции СТЬЮДРАСПРОБР, по заданному уровню значимости 1-α и n-1степени свободы  ищут симметричную критическую точку распределения  t _1-α=к₂, к₁=-к₂ . В том случае, когда | Z^*| < к₂ , принимают основную гипотезу. Если же | Z^*| > к₂ принимают альтернативную гипотезу, основную отклоняют, то есть при указанной альтернативной гипотезе критическая область является двусторонней.

     Следует иметь в виду, что когда альтернативная гипотеза Н_а имеет вид:

Н_а: m > m₀  или  H_a: m < m_{0 ,} критические области будут соответственно право и левосторонними. Поэтому границу области ищут по таблицам распределения Стьюдента, в которых указано «односторонняя». В первом случае принимают основную гипотезу, еслиZ^*<к₂, во втором случае принимают основную гипотезу, если Z^*>к₁.

Для второго параметра – дисперсии, формулируют следующую основную гипотезу:

                                                     H₀: s²=s²₀,

                                                     H_a: s²¹s²₀.

     Проверка основной гипотезы основана на теореме о том, что если основная гипотеза верна, то следующая выборочная статистика

                                            ·       

распределена по закону χ² с n-1 cтепенью свободы. Критическая  область будет являться двусторонней, ее границы к₁ и к₂ ищут из условия:

                                               

по таблицам критических точек распределения χ² или при помощи встроенной функции ХИ2ОБР.

     Если выборочная статистика удовлетворяет неравенству  к₁<Z^*<к₂, то принимают основную гипотезу, в противном случае принимают альтернативную гипотезу.