Статистическое моделирование. Построение статистических рядов и функций, страница 5

·            F _ξ (x)= Р{ξ < x}.

     Эта функция определена для всех вещественных х и принимает значения из промежутка [0;1]. Характерной особенностью в поведении этой функции является то, что она является неубывающей.

     Функцию распределения случайной дискретной величины, принимающей конечное число значений х₁, х₂,…, х_n, находят по следующему алгоритму:

                  ·               

     К закону распределения случайной непрерывной величины помимо функции распределения относят также плотность распределения вероятностей f_ξ(x). Функция распределения и плотность распределения связаны друг с другом следующим образом:

                          ·                   .

     В точках непрерывности функцииf_ξ(x)  имеет место, следующее равенство:

·          f_ξ(x)  =F¢_ξ (x).

     Плотность распределения вероятностей  всегда неотрицательна и удовлетворяет свойству, которое называют свойством нормировки:

                                       ·         .

     Все перечисленные виды законов распределения являются теоретическими. Математическая статистика оперирует с их эмпирическими аналогами, называемыми статистическими законами распределения.

      Построение эмпирических законов распределения  основано на законе больших чисел. Одна из основных теорем закона больших чисел устанавливает сходимость по вероятности относительной частоты случайного события Р*_n(A) к вероятности этого случайного  события Р(А).

     Именно поэтому теоретические вероятности Р{ξ=x_i}=p_i, из таблицы распределения случайной дискретной величины,   заменяют на относительную частоту случайного события {ξ=x_i}, которую вычисляют по формуле:  . В последнем равенстве через k_i  обозначена частота повторения в выборке значения х_i.

       Таким образом, когда изучаемая случайная величина дискретная,  для неё вместо ряда распределения строят сгруппированный статистический ряд, т. е. таблицу вида:

                                        ...                 

           ·                            ...            ,  ,      .

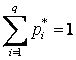Здесь  неповторяющиеся выборочные значения случайной величины x, расположенные в порядке возрастания, эточисло, показывающее, сколько раз значение  встретилось в выборке (частота выборочного значения),   объём выборки.