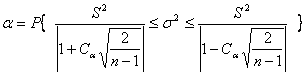Статистическое моделирование. Построение статистических рядов и функций, страница 18

                  ·    ,

                  ·  .

Через m обозначено неизвестное математическое ожидание Е[ξ], а через s²  неизвестная дисперсия  V [ξ] .

        Значение симметричной квантили  порядка α, стоящей в правых частях обоих неравенствах, ищется по таблицам Лапласа из уравнения ,  где параметр     это заданная доверительная вероятность.

Следующие  формулы применяют в том случае, когда оценки неизвестных числовых характеристик находят по выборкам малого объема.

·    ,

·  .

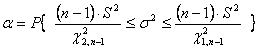Через  обозначено значение случайной величины, распределённой по закону Стьюдента с  степенью свободы (значение симметричной квантили распределения порядка α), которое находят по таблицам Стьюдента по доверительной вероятности  и числу степеней свободы  (n-1)  из условия: 

                    ·       .

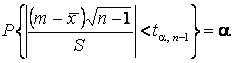Во второй формуле через  обозначено меньшее, а через  большее значение случайной величины, распределённой по закону хи-квадрат с  степенями свободы. Эти значения находят по таблицам  по доверительной вероятности  и числу степеней свободы из условия:

· .

Величины  и  это критические точки распределения хи-квадрат порядка  (1-α)/2 и (1+α)/2 соответственно.

В случае если заданы точность оценки  и надёжность (доверительная вероятность), объём выборки n, необходимый для достижения  заданной точности, находят по формулам:

а) для математического ожидания   ;

б) для дисперсии   .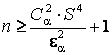

             5.2  Нахождение критических точек и квантилей распределения

                                    средствами MS-Excel

Для  нахождения критических точек распределения , и симметричной квантили  средствами MS-Excel можно воспользоваться следующими встроенными функциями категории Статистические.

· ХИ2ОБР (вероятность; степени свободы) позволяет определить значение критической точки распределения по двум входным параметрам: заданной вероятности  и указанному числу степеней свободы.

 Так как  объем выборки моделируемой случайной величины  равен n, то число степеней свободы, при обращении к функции ХИ2ОБР, берется равным n-1.

Например, пусть доверительная вероятность α=0,95, тогда для поиска   и  при помощи функции ХИ2ОБР сначаланужнорассчитать

                     ·