Статистическое моделирование. Построение статистических рядов и функций, страница 15

Так как 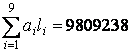 ,  то  =. Значит, =2221,295.   Чтобы вычислить выборочную дисперсию по формуле (1.1.6), просуммируем результаты вычислений в последнем столбце, получим: 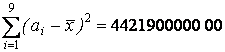. Следовательно, . В результате получаем: .▲

Для  случайных  непрерывных величин есть еще два теоретических показателя, связанных с моментами третьего и четвертого порядка. Первый из них это коэффициент асимметрии, он характеризует расположение графика плотности  распределения относительно математического ожидания. Если график плотности расположен симметрично относительно математического ожидания, то коэффициент асимметрии равен нулю. Положительное значение коэффициента асимметрии соответствует тому, что график плотности распределения смещен вправо относительно математического ожидания, отрицательное значение этой характеристики соответствует тому, что график плотности смещен влево относительно математического ожидания.

Эксцесс служит для характеристики  островершинности графика плотности распределения по сравнению с графиком плотности нормального распределения. Если величина эксцесса положительна, то график плотности более островершинный, чем нормальная кривая, если эксцесс отрицательный, то график плотности распределения является более плосковершинным по сравнению с нормальной кривой.

     Оценки асимметрии и эксцесса, вычисляемые по сгруппированному и интервальному ряду соответственно, имеют вид:

  ·       ,            ·        ,

  ·    ,           ·      .

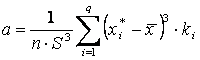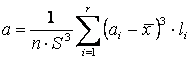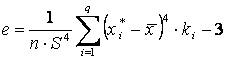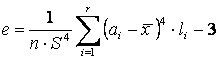 Оценки асимметрии и эксцесса характеризуют уже не график плотности распределения, а расположение гистограммы, ее смещение вправо или влево относительно выборочного среднего и ее остро или плосковершинность.

         4.2   Получение выборочных числовых характеристик

                                    средствами MS-Excel

Рассмотрим некоторые из встроенных функций категории Статистические, с помощью которых можно получать выборочные числовые характеристики.

·  СРЗНАЧ (число1, число2,…) возвращает оценку математического ожидания случайной величины ξ (значение ).

·  СКОС (число1; число2;…) возвращает оценку а коэффициента асимметрии распределения. В качестве аргументов функции можно использовать массив чисел или ссылку на массив.

·  ДИСП (число1; число2;…)  возвращает несмещенную оценку дисперсии (значение S²). ДИСП предполагает, что аргументы являются числовыми, если аргументы логические значения или текст, то следует использовать функцию ДИСПА.

·  ДИСПА (значение1, значение2,…) возвращает несмещенную оценку дисперсии по выборке. Аргументы функции, содержащие значение ИСТИНА интерпретируются как 1, аргументы, содержащие текст или значение ЛОЖЬ интерпретируются как 0 (ноль).

·  ДИСПР (число1, число2,…) вычисляет смещенную оценку дисперсии (значение), логические значения и текст игнорируются.

·  ДИСПРА (значение1, значение2,..) вычисляет смещенную оценку дисперсии, учитываются текстовые и логические значения.

·  ЭКСЦЕСС (число1, число2,..) возвращает оценку коэффициента эксцесса ( значение величины е). Аргументы должны быть числами или ссылками на числовой массив, текст и логические значения игнорируются, нулевые значения учитываются.