Теория контроля контактных схем, страница 8

          Например, для неисправности  имеем (см. формулы (3.1) и (3.8)):

= {0, 1, 5, 10, 11, 12, 14, 15, 26, 30}.

Функция  задана в табл. 3.9.

          Введем обозначения:  и .

Тогда,

.                                             (3.9)

Функция  определяет разрешенные наборы, которые в результате возникновения неисправности становятся запрещенными (в рассмотренном примере это наборы 10, 11, 12, 14, 15). Функция  определяет запрещенные наборы, которые в результате возникновения неисправности становятся разрешенными (0, 1, 5, 26, 30). Очевидно, что

 × = 0,

и  функции    и   могут рассчитываться независимо друг от друга.

          Используя ЭНФ и ОЭНФ, функции   и   рассчитываются по формулам:

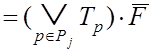,                                (3.10)

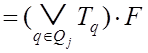,                                (3.11)

где  – номер конъюнкции ЭНФ (ОЭНФ);

 – множество номеров конъюнкций ЭНФ (ОЭНФ), содержащих буквы из множества  и не содержащих буквы из множества ;  – функция, реализуемая конъюнкцией ЭНФ (ОЭНФ) с номером  в результате приравнивания 1 в ней букв из множества .

          Рассмотрим неисправность . Ее проекция на ЭНФ (3.3) имеет вид:

                                1         2         3         4         5           6        

.           (3.12)

                           0            0                        1                        1

Поэтому имеем: {4, 6},

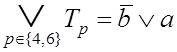
и, согласно формулам (3.10) и (3.2),

 =

 {0, 1, 5, 26, 30}.

Проекция  на ОЭНФ (3.4) имеет вид:

            1             2               3              4                  5              6 

.    (3.13)

      1        0       1              0      0         0              0       0         0   

Поэтому имеем: {2}

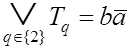
и, согласно формулам (3.11) и (3.1),

=

 {10, 11, 12, 14, 15}.

          При вычислении функций  и  нет необходимости предварительно вычислять функции  и . Так как последние задаются ЭНФ и ОЭНФ и, учитывая, что конъюнкции ЭНФ и ОЭНФ попарно ортогональны, формулы (3.10) и (3.11) можно представить в следующем виде:

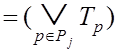
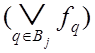,                              (3.14)

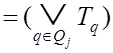
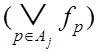,                             (3.15)

где  – функция, реализуемая конъюнкцией ЭНФ (ОЭНФ) с номером ;

        – множество номеров конъюнкций ОЭНФ (ЭНФ), содержащих буквы из множества .

          Для  неисправности    имеем:   = {1, 3, 4, 5, 6}  и  = {1, 2}. Поэтому

 =

 {0, 1, 5, 26, 30}.

 {10, 11, 12, 14, 15}.

          Нетрудно построить алгоритмы реализации формул (3.14) и (3.15) по матрице совместимости и по матрице отношений.

3.5. Отношения между неисправностями в контактных схемах

          В табл. 3.10 приведены два вида отношений между неисправностями в контактных схемах. Неисправности  и  являются эквивалентными (), если их проверяющие функции равны. Это означает, что любой тестовый набор, который обнаруживает , обнаруживает и  (и наоборот). Поэтому при построении теста одну из этих неисправностей можно исключить из списка рассматриваемых.

Т а б л и ц а   3.10

Наименование отношения	Обозначение	Связь между проверяющими функциями
Эквивалентность
Включение

          Неисправность  находится в отношении включения к неисправности  (), если проверяющая функция  находится в отношении импликации к функции . Это означает, что любой тестовый набор, который обнаруживает , обнаруживает и , но обратное не имеет место. Поэтому при построении теста неисправность  можно исключить из рассмотрения.

          Исследования показывают, что в реальных схемах число неисправностей, которые находятся в отношениях эквивалентности и включения очень велико, особенно среди кратных неисправностей. Поэтому сокращение списка рассматриваемых неисправностей является эффективным средством уменьшения вычислений при построении проверяющего теста.

          Существует связь отношений между контактами с отношениями  между  неисправностями  этих  контактов  (табл. 3.11). Пусть