Теория контроля контактных схем, страница 15

          Завершение процесса формирования полного контрольного списка неисправностей определяет следующая теорема, непосредственно вытекающая из указанных следствий.

          Теорема 3.7. Если в неизбыточной контактной схеме контрольный список неисправностей кратности  является пустым и число  кратно числу четыре, то являются пустыми и все контрольные списки неисправностей кратности больше .

          Алгоритм 3.4. (Формирование полного контрольного списка неисправностей контактной схемы).

          1. Формируется множество .

          2. С помощью теоремы 3.3 формируется множество .

          3.  = 4.               

          4. Является ли число  кратным числу четыре? Если да, то переход к п. 5. Если нет, то переход к п. 6.

          5. ? Если да, то переход к п. 13. Если нет, то переход к п. 6.

          6.  =  + 1.

          7. Формируется множество  из множества  с помощью теоремы 3.4.

          8. Является ли число  кратным числу четыре? Если да, то переход к п. 9. Если нет, то переход к п. 10.

          9. Формируется множество  из множества  с помощью теоремы 3.6. Переход к п. 12.

          10. Является ли число  кратным числу два? Если да, то переход к п. 11. Если нет, то переход к п. 12.

          11. Формируется множество  из множества  с помощью теоремы 3.6.

          12. Формируется множество . Переход к п. 4.

          13. Конец.

          В табл. 3.19 приведены результаты применения алгоритма 3.4 к  схеме,  представленной  на  рис. 3.14  и  содержащей 16 контактов.

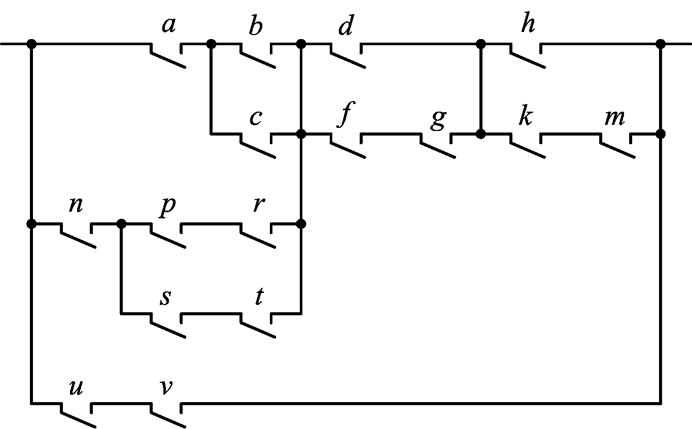
Рис3.14. Схема, содержащая 16 контактов

В ней контрольные списки при  являются пустыми. Полный контрольный список схемы содержит 957 неисправностей, что составляет 0,0022% от общего числа неисправностей.

          Главный вывод, вытекающий из результатов данного раздела, состоит в том, что одиночные тесты имеют высокую обнаруживающую способность. Во-первых, они обнаруживают все неисправности двух и трех контактов. Во-вторых, с увеличением кратности резко уменьшается процент неисправностей, которые могут быть не обнаружены  одиночным  тестом  или тестом, построенном для неисправ-

Т а б л и ц а   3.19

Кратность неисправности	Общее число неисправностей данной кратности	Число неисправностей контрольного списка	Процент
1	32	23	71,8
4	29120	108	0,3
5	139776	208	0,143
6	512512	244	0,047
7	1464320	240	0,016
8	3294720	142	0,0043
9	5857280	32	0,00055
1–16	3 = 43046720	957	0,0022

ностей меньших кратностей. Поэтому в практических приложениях для контроля контактных схем часто ограничиваются построением одиночных тестов. Два метода построения одиночного теста рассматривается в следующем разделе.

3.7. Методы построения одиночных тестов контактных схем

          Минимальный одиночный тест контактной схемы строится путем перечисления всех неисправностей списка  по следующему алгоритму.

          Алгоритм 3.5. (Построение одиночного проверяющего теста).

          1. Определить множество  с использованием отношений табл. 3.13.

          2. Для каждой неисправности из  вычислить проверяющую функцию с помощью формул (3.10)–(3.15) или с помощью алгоритма 3.3.

          3. Составить таблицу покрытия и найти минимальный тест.

          Пример 3.2. Построить одиночный проверяющий тест для схемы рис. 3.15.

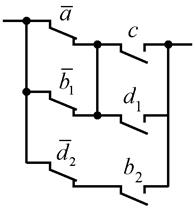
Рис.3.15. Схема из примера 3.2

Множество  = ,,,,,,,,. Эквивалентные формы схемы имеют вид

,

 .

Используя формулы (3.14) и (3.15), получаем

Решение задачи покрытия можно находить раздельно для запрещенных  наборов (табл. 3.20)  и  для   разрешенных  наборов (табл. 3.21).