Теория контроля контактных схем, страница 3

          С помощью данных отношений вводится самая компактная форма представления параллельно-последовательных контактных схем в виде матрицы отношений (МО) [24]. Матрица отношений представляет собой таблицу, содержащую три столбца и n – 1 строку (см. табл. 3.5). В крайних столбцах записываются обозначения контактов, а в среднем столбце – отношение между ними. Заполнение матрицы начинается с верхней строки. Для этого в исходной схеме находится пара контактов (любая), включенная последовательно или параллельно, т.е. находящихся в отношении эквивалентности или замены.  Это  отношение  записывается  в  первой  строке матрицы. В рассматриваемой схеме (рис. 3.1) существует отношение  « , которое записано в первой строке табл. 3.5. В последующих

                                              Т а б л и ц а   3.5

строках сверху вниз в любом порядке записываются все другие отношения эквивалентности и замены, существующие в исходной схеме.  В  схеме  (рис. 3.1)  имеются  еще  два  отношения: «,  = . Расположение обозначений контактов в левом или правом крайних столбцах таблицы безразлично. Затем из исходной схемы исключаются контакты, обозначение которых расположено в правом столбце, в результате чего получают упрощенную схему (рис. 3.5, а).

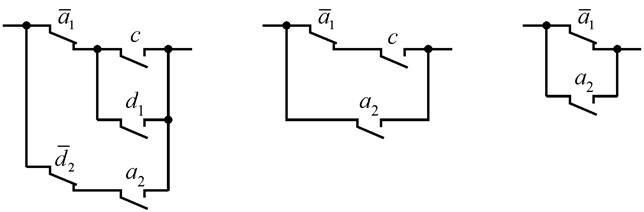
Рис.3.5. Этапы сокращения контактной схемы

В  ней  возникают  новые отношения эквивалентности и замены, которые аналогичным образом записываются в таблицу. В схеме (рис. 3.5,а) имеются отношения  = ,  « , которые записаны в четвертой и пятой строках табл. 3.5. Процесс построения МО завершается, когда в результате сокращений получают схему, содержащую два контакта (рис. 3.5, в). Отношение между ними записывается в последней строке.

          МО полностью задает структуру контактной схемы, так как по ней однозначно можно построить данную схему и ее ЭНФ с помощью процесса, обратного описанному выше. Построение ЭНФ начинается с нижней строки и при переходе вверх в новую строку в формулу добавляется буква, находящаяся в правом столбце. Для табл. 3.5 имеем:

=

=                 (3.5)

Формулы (3.5) и (3.3) совпадают.

          Достоинством МО является то, что размеры ее лишь линейно растут с увеличением числа путей схемы n. Сравним сложность ЭНФ,  МС  и  МО для контактной структуры на рис. 3.4 для m = 10 (n = 20). Будем оценивать сложность числом клеток соответствующих  таблиц.  ЭНФ  задается троичной таблицей с числом столбцов n  и  числом  строк, равным числу конъюнкций. Тогда для схемы рис. 3.4 сложность ЭНФ равна  = 20  = 20480. Число клеток МС равно , но поскольку МС симметрична относительно левой главной диагонали (см. табл. 3.1), в памяти ЭВМ достаточно хранить половину матрицы. Тогда сложность МС равна 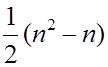 = 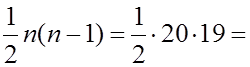190. Сложность МО равна 57. Сложность МС и МО в данном случае примерно в 100 и 400 раз меньше, чем сложность ЭНФ.

3.2. Неисправности в контактных схемах

          В контактных схемах наиболее вероятным является появление в процессе эксплуатации неисправностей следующих видов: обрыв контакта, короткое замыкание контакта, ложное несрабатывание или срабатывание реле, обрыв соединительного провода. В процессе монтажа могут возникнуть также случаи лишних соединений между проводами и перепутывания проводов.

          Неисправности  контакта  а  типа  «короткое  замыкание» и «обрыв» обозначим соответственно как  и . Кратную неисправность  нескольких  контактов будем обозначать через , причем  = , где  – множество контактов с неисправностью «обрыв»,  – множество контактов с неисправностью «короткое замыкание»,  – порядковый номер неисправности.

          Поскольку   каждый  контакт  может  иметь  три  состояния  (исправное и два неисправных), то общее число кратных неисправностей в схеме с  nконтактами

,                                           (3.6)