Другие предметы \ Основы теории надежности

Теория контроля контактных схем, страница 4

а общее число неисправностей кратности k подсчитывается по формуле:

. (3.7)

Например, для схемы (рис. 3.1) общее число неисправностей равно = 5660, число одиночных неисправностей – 16, двойных – 112 и т.д.

Рассмотрим влияние неисправностей на работу контактных схем. Как известно [25], замыкающий контакт реле реализует логическую функцию «повторение», а размыкающий контакт – функцию «отрицание». Поэтому возникновение физических неисправностей типа «обрыв» или «короткое замыкание» можно интерпретировать как изменение логической функции, реализуемой контактом. А именно, неисправный контакт реализует функции «константа О» (при обрыве) и «константа 1» (при коротком замыкании). По этой причине указанные неисправности называют константными логическими неисправностями.

Их возникновение, в свою очередь, приводит к тому, что функция алгебры логики (ФАЛ) , вычисляемая схемой с неисправностью , отличается от ФАЛ F исправной схемы. Например, найдем функции для неисправностей и в схеме (рис. 3.1). Из формулы (3.1) получаем

Нетрудно видеть, что и . Это означает, что неисправность типа «обрыв» уменьшает число двоичных наборов, на которых функция равна 1, а неисправность типа «короткое замыкание», наоборот, увеличивает их число.

Из рассмотренного примера виден смысл введения понятия константной логической неисправности. Она является математической моделью физической неисправности. Моделирование заключается в «проекции» неисправности на логическую формулу путем фиксации ее букв в 0 или 1. Это относится и к кратным неисправностям. Например, для неисправности третьей кратности имеем:

. (3.8)

Неисправности типа ложное включение или невключение реле и большинство обрывов соединительных проводов также могут задаваться моделью константных неисправностей. Например, ложное включение (невключение) реле а в схеме рис. 3.1 описывается неисправностью кратности два , а обрыв провода между контактом и полюсом 2 – неисправностью .

Лишние провода, перепутывание проводов, а также некоторые обрывы являются «нелогическими» неисправностями в том смысле, что они не могут быть смоделированы фиксацией в 0 или 1 букв логической формулы. Это существенно осложняет способы их обнаружения и локализации.

3.3. Вычисление проверяющих функций

для неисправностей контактов

Сформулируем условия обнаружения одиночной неисправности контакта. Чтобы обнаружить обрыв некоторого контакта необходимо и достаточно обеспечить выполнение двух условий: 1) создать хотя бы один путь проводимости схемы, проходящий через контакт ; 2) создать хотя бы одно урезанное сечение схемы, проходящее через контакт (то есть сечение, в котором исключено состояние контакта ). Тогда при отсутствии неисправности схема будет замкнута, а при наличии неисправности – разомкнута.

На рис. 3.6 показаны условия обнаружения обрыва контакта в схеме рис. 3.1.

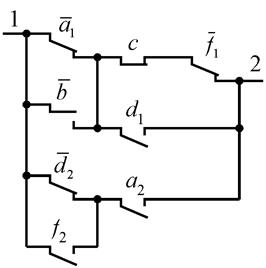
Рис.3.6. Условия обнаружения обрыва контакта

При подаче на вход схемы двоичного набора abcdf = 01100 существует путь и урезанное сечение . Набор 01100 является разрешенным (F = 1), а при наличии обрыва становится запрещенным (F* = 0). Такой набор называется тестовым относительно данной неисправности. Все множество тестовых наборов образуют проверяющую функцию неисправности .