Теория контроля контактных схем, страница 10

Среди букв ЭНФ существуют следующие отношения: , , , , , , , , , . Относительно ОЭНФ эти отношения двойственны.

          Так как для указанных неисправностей  и  имеем: ,  и буквы ,  и   несовместимы с буквами ,  то условия теоремы 3.1 выполняются. Поэтому,   . В самом деле, используя формулы (3.10) и (3.11), получаем

,
.

          Для следующих двух неисправностей условия теоремы 3.1 не выполняются:  и . Так как буква  совместима с буквой , то четвертое условие не выполняется и   .  В самом деле,

;

.

          Для эквивалентных неисправностей можно сформулировать более простые условия, как следствие из теоремы 3.1.

          Теорема 3.2. , если

          1) ;

2) .

          Например, эквивалентными являются неисправности  и .

3.6. Формирование контрольных списков неисправностей

контактов

          В данном разделе рассматриваются методы сокращения списков неисправностей контактов. Такое сокращение является эффективным способом уменьшения объемов вычислений в процедурах, связанных с перечислением неисправностей.

          Определение 3.2. Полным контрольным списком неисправностей контактной схемы называется множество неисправностей, обнаружение которых обеспечивает обнаружение любой одиночной или кратной неисправности контактов.

          Определение 3.3. Контрольным списком неисправностей кратности  называется множество таких неисправностей  этой кратности, что не существует ни одной неисправности меньшей кратности  такой, что .

          Контрольный список неисправностей кратности  будем обозначать через . Смысл введения этого понятия состоит в том, что, если некоторая неисправность , то она не входит и в полный контрольный список, так как обнаруживается любым проверяющим тестом, построенным для неисправностей меньших кратностей. Если же неисправность , то она может быть не обнаружена хотя бы одним таким тестом.

          Согласно определению 3.3 множество  является единственным. Его сложно найти. Более просто находятся некоторые избыточные, но существенно сокращенные, списки неисправностей, содержащие в себе указанные множества. Их также будем называть просто контрольными списками.

          Формирование полного контрольного списка начинается с построения множества . При этом используется связь отношений между контактами с отношениями между их неисправностями в соответствии с табл. 3.13.

                                                                                            Т а б л и ц а   3.13

          В схеме, приведенной на рис. 3.12. имеют место следующие отношения: , ,  , , , , , , , , , , . Поэтому, ,.

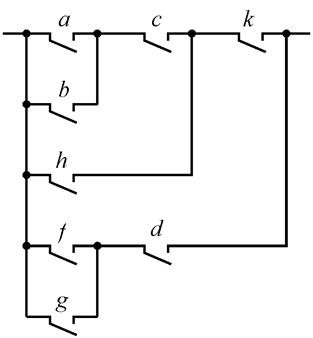
Рис.3.12. Контактная схема