Теория контроля контактных схем, страница 5

Таким образом, обрыв контакта  обнаруживается на 5 тестовых наборах. Указаны десятичные эквиваленты этих наборов (а – старший разряд).

          Чтобы обнаружить короткое замыкание некоторого контакта  необходимо и достаточно обеспечить выполнение двух условий: 1) создать хотя бы одно сечение схемы, проходящее через контакт ; 2) создать хотя бы один урезанный путь, проходящий через контакт  (то есть путь, в котором исключено состояние контакта ). Тогда при отсутствии неисправности схема будет разомкнута, а при наличии неисправности – замкнута.

          На рис. 3.7 приведены условия обнаружения короткого замыкания контакта  в схеме рис. 3.1.

Рис.3.7. Условия обнаружения короткого замыкания контакта

 При подаче на вход схемы двоичного   набора   abcdf = 11010   существует  сечение  и урезанный  путь . Набор 11010 является запрещенным (F= 0),  а  при  наличии неисправности становится разрешенным (F* = 1).

          Алгоритм 3.2. (Вычисление проверяющей функции неисправности типа короткое замыкание контакта ).

          1. Выписывается дизъюнкция всех конъюнкций ОЭНФ (сечений) , содержащих букву .

          2. Выписывается дизъюнкция всех урезанных конъюнкций ЭНФ (путей) , содержащих букву .

          3. Исключаются индексы букв ЭНФ и находится проверяющая функция  =× .

          Для       неисправности             (рис.    3.1)      имеем:      =

, , =

=  Таким образом, короткое замыкание контакта  обнаруживается на двух тестовых наборах.

          Как видно из алгоритмов 3.1 и 3.2 для вычисления проверяющих функций неисправностей контактов не требуется знать всю ЭНФ, которая может иметь слишком большие размеры. Достаточно знать только те конъюнкции, на которые «проектируется» данная неисправность. Эти конъюнкции могут быть рассчитаны по МС и ОМС (без расчета всей ЭНФ).

          Для неисправности  выражение  находится после сокращения МС (табл. 3.1) путем исключения всех строк и столбцов, соответствующих контактам, которые несовместимы с контактом  (см. табл. 3.6). Табл. 3.6 содержит две полные подматрицы:  и . Аналогично,  выражение  находится  по  сокращенной ОМС

Т а б л и ц а   3.7

(табл. 3.7). Табл. 3.7 содержит две полные подматрицы:  и .

          Еще более простой алгоритм вычисления проверяющей функции неисправности контакта существует с использованием матрицы отношений [24]. Обозначение этого контакта должно быть записано в клетке левого крайнего столбца последней строки.

          Например,  в  табл. 3.8, которая  является  МО  для  схемы  рис. 3.8, в этой клетке записано обозначение контакта а.

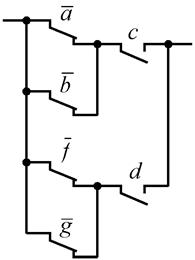
Рис.3.8. Контактная схема

Этапы сокращения схемы показаны на рис. 3.9.

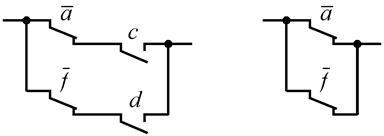
Рис.3.9. Этапы сокращения контактной схемы

                                       Т а б л и ц а   3.8

Идея алгоритма состоит в следующем. Рассматриваются последняя строка  МО  и соответствующая ей последняя схема разложения (рис. 3.9,б). Составляется выражение Р, состоящее из букв ЭНФ и определяющее условие проверки данной неисправности (знаки инверсий у размыкающих контактов не учитываются). Например, в схеме рис. 3.9, б для неисправности контакта а (обрыва или короткого замыкания) имеем: . Знак инверсии означает, что контакт f должен быть разомкнут, чтобы проверить контакт а.